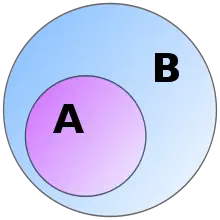
子集

假设有${\displaystyle A}$和${\displaystyle B}$两个集合，如果${\displaystyle A}$中的每个元素都是${\displaystyle B}$的元素，则：

• ${\displaystyle A}$是${\displaystyle B}$的 子集，记作 ${\displaystyle A\subseteq B}$

也可以说

• ${\displaystyle B}$是${\displaystyle A}$的 超集，记作 ${\displaystyle B\supseteq A}$

如果${\displaystyle A}$是${\displaystyle B}$的子集，但${\displaystyle A}$不等于${\displaystyle B}$（即${\displaystyle B}$中至少存在一个元素不在${\displaystyle A}$集合中），则：

• ${\displaystyle A}$是${\displaystyle B}$的 真子集，记作 ${\displaystyle A\subsetneqq B}$

也可以说

• ${\displaystyle B}$是${\displaystyle A}$ 的 真超集，记作 ${\displaystyle B\supsetneqq A}$

符号${\displaystyle \subseteq }$表示任何子集关系，符号${\displaystyle \subsetneqq }$表示真子集关系。${\displaystyle \subset }$也是一个很常見的符号，但其含义容易混淆。

有人用${\displaystyle \subset }$和${\displaystyle \supset }$表示任何子集和超集关系，即${\displaystyle \subseteq }$和${\displaystyle \supseteq }$所分别代表的含义。[1][2][3]所以在这些作者的文章中，对于任意集合${\displaystyle A}$，${\displaystyle A\subset A}$ 始终成立。

也有人用${\displaystyle \subset }$和${\displaystyle \supset }$表示真子集和真超集的概念，即${\displaystyle \subsetneqq }$和${\displaystyle \supsetneqq }$所分别代表的含义。[4]^:p.6这样${\displaystyle \subseteq }$和${\displaystyle \subset }$就类似于不等符号${\displaystyle \leq }$和${\displaystyle <}$的关系。例如如果 ${\displaystyle x\leq y}$，那么${\displaystyle x}$可能等于${\displaystyle y}$也可能不等于，而如果 ${\displaystyle x<y}$，那么${\displaystyle x}$就一定不等于${\displaystyle y}$。换用${\displaystyle \subset }$表示真子集，如果 ${\displaystyle A\subseteq B}$，那么${\displaystyle A}$可能等于${\displaystyle B}$也可能不等于，而如果 ${\displaystyle A\subset B}$，那么${\displaystyle A}$就一定不等于${\displaystyle B}$。

ISO 80000-2 标准中定义了两种符号搭配：使用${\displaystyle \subseteq }$表示子集关系，${\displaystyle \subset }$表示真子集关系；或者使用${\displaystyle \subset }$表示子集关系，使用${\displaystyle \subsetneqq }$表示真子集关系。

• 集合${\displaystyle \left\{1,2\right\}}$是集合${\displaystyle \left\{1,2,3\right\}}$的真子集。
• 自然数集合是有理数集合的真子集。
• 集合${\displaystyle \{x:x}$是大于2000的素数${\displaystyle \}}$是集合${\displaystyle \{x:x}$是大于1000的奇数${\displaystyle \}}$的真子集。
• 任意集合是其自身的子集，但不是真子集。
• 空集，写作 ${\displaystyle \varnothing }$，是任意集合${\displaystyle X}$的子集。空集总是其他集合的真子集，除了其自身。

命题1：空集是任意集合的子集。

这个命题说明：包含是一种偏序关系。

命题2：若${\displaystyle A,B,C}$是集合，则：

自反性：

• ${\displaystyle A\subseteq A}$

反对称性：

• ${\displaystyle A\subseteq B}$且${\displaystyle B\subseteq A}$当且仅当${\displaystyle A=B}$

传递性：

• 若${\displaystyle A\subseteq B}$且${\displaystyle B\subseteq C}$则${\displaystyle A\subseteq C}$

这个命题说明：对任意集合${\displaystyle S}$，${\displaystyle S}$的幂集按包含排序是一个有界格，与上述命题相结合，则它是一个布尔代数。

命题3：若${\displaystyle A,B,C}$是集合${\displaystyle S}$的子集，则：

存在一个最小元和一个最大元：

• ${\displaystyle \varnothing \subseteq A\subseteq S}$（ ${\displaystyle \varnothing \subseteq A}$由命題1給出）

存在并运算：

• ${\displaystyle A\subseteq A\cup B}$
• 若${\displaystyle A\subseteq C}$且${\displaystyle B\subseteq C}$则${\displaystyle A\cup B\subseteq C}$

存在交运算：

• ${\displaystyle A\cap B\subseteq A}$
• 若${\displaystyle C\subseteq A}$且${\displaystyle C\subseteq B}$则${\displaystyle C\subseteq A\cap B}$

命题4:对任意两个集合${\displaystyle A}$和${\displaystyle B}$，下列表述等价：

• ${\displaystyle A\subseteq B}$
• ${\displaystyle A\cap B=A}$
• ${\displaystyle A\cup B=B}$
• ${\displaystyle A-B=\varnothing }$
• ${\displaystyle B\subseteq A'}$

这个命题说明：表述"${\displaystyle A\subseteq B}$"，和其他使用并集，交集和补集的表述是等价的，即包含关系在公理体系中是多余的。

• 冪集：某集合的全部子集组成的集合。