磁矩
磁矩是磁鐵的一種物理性質。處於外磁場的磁鐵,會感受到力矩,促使其磁矩沿外磁場的磁場線方向排列。磁矩可以用向量表示。磁鐵的磁矩方向是從磁鐵的指南極指向指北極,磁矩的大小取決於磁鐵的磁性與量值。不只是磁鐵具有磁矩,載流迴路、電子、分子或行星等等,都具有磁矩。
科學家至今尚未發現宇宙中存在有磁單極子。一般磁性物質的磁場,其泰勒展開的多極展開式,由於磁單極子項目恆等於零,第一個項目是磁偶極子項、第二個項目是磁四極子()項,以此类推。磁矩也分為磁偶極矩、磁四極矩等等部分。從磁矩的磁偶極矩、磁四極矩等等,可以分別計算出磁場的磁偶極子項目、磁四極子項目等等。隨著距離的增遠,磁偶極矩部分會變得越加重要,成為主要項目,因此,磁矩這術語時常用來指稱磁偶極矩。有些教科書內,磁矩的定義與磁偶極矩的定義相同[1]。
概述
一個載流迴圈的磁偶極矩是其所載電流乘以迴路面積:
- ;
其中,為磁偶極矩,為電流,為面積向量。磁偶極矩、面積向量的方向是由右手定則決定。
處於外磁場的載流迴圈,其感受到的力矩和其勢能與磁偶極矩的關係為:
- 、
- ;
其中,為力矩,為磁場,為勢能。
許多基本粒子,例如電子,都具有內稟磁矩。這種內稟磁矩是許多巨觀磁場力的來源,許多物理現象也和此有關。這種磁矩和古典物理的磁矩不同,而是和粒子的自旋有關,必須用量子力學來解釋。這些內稟磁矩是量子化的,最小的基本單位,常常稱為「磁子」()。例如,電子自旋的磁矩與波耳磁子的關係式為:
- ;
單位
採用國際單位制,磁偶極矩的因次是面積×電流。磁偶極矩的單位有兩種等價的表示法:
CGS單位制又可細分為幾種亞單位制:靜電單位制(),電磁單位制()、高斯單位制。
| 語言 | 國際單位制 | 靜電單位制 | 電磁單位制 | 高斯單位制 |
|---|---|---|---|---|
| 中文 | 1 安培·公尺2 = 1 焦耳/特斯拉 | = (103 c) 靜安培·公分2 | = (103) 絕對安培·公分2 | = (103) 爾格/高斯 |
| 英文 | 1 A·m2 =1 J/T | = (103 c) statA·cm2 | = (103) abA·cm2 | = (103) erg/Gauss |
磁偶極矩在電磁單位制與在靜電單位制的比例正好等於單位為公分/秒的光速。
在這篇文章內,所有的方程式都採用國際單位制。
兩種磁源
在任何物理系統裏,磁矩最基本的源頭有兩種:
- 電荷的運動,像電流,會產生磁矩。只要知道物理系統內全部的電流密度分佈(或者所有的電荷的位置和速度),理論上就可以計算出磁矩。
- 像電子、質子一類的基本粒子會因自旋而產生磁矩。每一種基本粒子的內稟磁矩的大小都是常數,可以用理論推導出來,得到的結果也已經通過做實驗核對至高準確度。例如,電子磁矩的測量值是−9.284764×10−24焦耳/特斯拉[3]。磁矩的方向完全決定於粒子的自旋方向(電子磁矩的測量值是負值,這意味著電子的磁矩與自旋呈相反方向)。
整個物理系統的淨磁矩是所有磁矩的向量和。例如,氫原子的磁場是以下幾種磁矩的向量和:
- 電子的自旋。
- 電子環繞著質子的軌域運動。
- 質子的自旋。
再舉個例子,構成條形磁鐵的物質,其未配對電子的內稟磁矩和軌域磁矩的向量和,是條形磁鐵的磁矩。
計算磁矩的方程式
平面迴圈
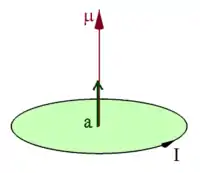
對於最簡單的案例,平面載流迴圈的磁偶極矩是
- ;
其中,是迴圈所載有的恆定電流,是平面迴圈的面積向量。
面積向量和磁偶極矩的方向是由右手定則給出:令四隻手指朝著電流方向彎曲,伸直大拇指,則大拇指所指的方向即是面積向量的方向,也是磁偶極矩的方向。
這有限面積的載流迴圈還有更高階的磁矩,像磁四極矩,磁八極矩等等。假設載流迴圈的面積趨向於零、電流趨向於無窮大,同時保持不變,則所有更高階的磁矩會趨向於零,這真實的載流迴圈趨向於理想磁偶極子,或純磁偶極子。
任意迴路
對於任意迴路案例,假設迴路載有恆定電流,則其磁偶極矩為
- ;
其中,是積分曲面,是邊緣的閉合迴路,是微小面積元素,是微小線元素,是的位置。
引用向量恆等式
- ,
即可得到磁偶極矩的路徑積分方程式
- 。
任意電流分佈
對於最廣義的任意電流分佈案例,磁偶極矩為
- ;
其中,是積分體積,是源電流位置,是電流密度,是微小體積元素。
任意一群移動電荷,像旋轉的帶電固體,都可以用這方程式計算出其磁偶極矩。
載流迴路產生的磁場
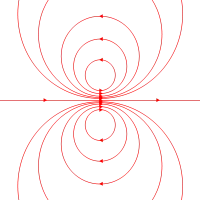
載流迴路會在周圍產生磁場。這磁場包括偶極磁場與更高次的多極項目。但是,隨著距離的增遠,這些多極項目會更快速地減小,因此,在遠距離位置,只有偶極項目是磁場的顯要項目。
思考一個載有恆定電流的任意局域迴路,其磁矢勢為
- ;
其中,是檢驗位置,是源頭位置,是微小線元素的位置,是磁常數。
假設檢驗位置足夠遠,,則表達式可以泰勒展開為
- ;
其中,是勒讓德多項式,是與之間的夾角。
所以,磁矢勢展開為
- 。
思考項目,也就是磁單極子項目:
- 。
由於閉合迴路的向量線積分等於零,磁單極子項目恆等於零。
再思考項目,也就是磁偶極子項目:
- 。
注意到磁偶極矩為,偶極磁矢勢可以寫為
- 。
偶極磁場為
- 。
由於磁偶極子的向量勢有一個奇點在它所處的位置(原點),必須特別小心地計算,才能得到正確答案。更仔細地推導,可以得到磁場為
- ;
其中,是狄拉克δ函數。
偶極磁場的狄拉克δ函數項目造成了原子能級分裂,因而形成了超精細結構()[5]。在天文學裏,氫原子的超精細結構給出了21公分譜線,在電磁輻射的無線電波範圍,是除了3K背景輻射以外,宇宙彌漫最廣闊的電磁輻射。從復合紀元()至再電離紀元()之間的天文學研究,只能依靠觀測21公分譜線無線電波。
給予幾個磁偶極矩,則按照疊加原理,其總磁場是每一個磁偶極矩的磁場的總向量和。
處於外磁場的磁偶極子
磁偶極子感受到的磁力矩
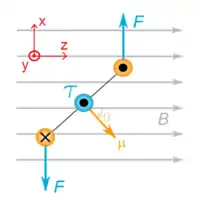
如圖右,假設載有電流的一個方形迴圈處於外磁場。方形迴圈四個邊的邊長為,其中兩個與平行的邊垂直於外磁場,另外兩個邊與磁場之間的夾角角弧為。
垂直於外磁場的兩個邊所感受的磁力矩為
- 。
另外兩個邊所感受的磁力矩互相抵消。注意到這迴圈的磁偶極矩為 。所以,這迴圈感受到的磁力矩為
- 。
令載流迴圈的面積趨向於零、電流趨向於無窮大,同時保持不變,則這載流迴圈趨向於理想磁偶極子。所以,處於外磁場的磁偶極子所感受到的磁力矩也可以用上述方程式表示。
當磁偶極矩垂直於磁場時,磁力矩的大小是最大值;當磁偶極矩與磁場平行時,磁力矩等於零。
磁偶極子的勢能
將載流迴圈從角弧扭轉到角弧,磁場所做的機械功為
- 。
注意到磁力矩的扭轉方向是反時針方向,而是朝著順時針方向遞增,所以必須添加一個負號。設定,則
- 。
對抗這磁場的磁力矩,將載流迴圈從角弧扭轉到角弧,所做的機械功為
- 。
定義載流迴圈的勢能等於這機械功,以方程式表示為
- 。
與前段所述同理,磁偶極子的勢能也可以用這方程式表示。當磁偶極矩垂直於磁場時,勢能等於零;當磁偶極矩與磁場呈相同方向時,勢能是最小值;當磁偶極矩與磁場呈相反方向時,勢能是最大值。
非均勻磁場
假設外磁場為均勻磁場,則作用於載流迴路的磁場力等於零:
- 。
假設外磁場為非均勻的,則會有一股磁場力,作用於磁偶極子。依照磁矩模型的不同,求得的磁場力也會不同[6]。採用常見的「電流模型」,則一個磁偶極子所感受到的磁場力為
- 。
另外一種採用「磁荷模型」。這類似電偶極矩的模型,計算出的磁場力為
- 。
兩者之間的差別為
- 。
假設,電流等於零,電場不含時間,則根據馬克士威-安培方程式,
- ,
兩種模型計算出來的磁場力相等。可是,假設電流不等於零,或電場為含時電場,則兩種模型計算出來的磁場力不相等。1951年,兩個不同的實驗,研究中子的散射於鐵磁性物質,分別得到的結果與電流模型預估的結果相符合[6]。
範例
圓形載流迴圈的磁偶極矩
一個載流迴圈的磁偶極矩與其面積和所載電流有關。例如,載有1安培電流,半徑為0.05公尺的單匝圓形載流迴圈,其磁偶極矩為:
- 。
磁偶極矩垂直於載流迴圈的平面。載流迴圈的磁矩,可以用來建立以下幾點論據:
- 假設場位置的距離超遠於迴圈半徑,則磁場會呈反立方減弱:
- 沿著迴圈的中心軸,磁矩與場位置平行:
- 。
- 在包含迴圈的平面的任意位置,磁矩垂直於場位置:
- 。
- 負號表示平面任意位置案例與中心軸案例,這兩個案例的磁場呈相反方向。
- 沿著迴圈的中心軸,磁矩與場位置平行:
- 。
- 應用力矩的觀念,可以製造出羅盤。假設這羅盤的磁針,由於力矩的作用,從磁針的磁矩垂直於地磁場,旋轉至磁針的磁矩與地磁場呈相同方向,則這羅盤-地球系統釋放出的能量為
- 。
- 由於羅盤懸浮系統的摩擦機制,這能量是以熱量的形式耗散淨盡。
螺線管的磁矩
.svg.png.webp)
一個多匝線圈(或螺線管)的磁矩是其每個單匝線圈的磁矩的向量和。對於全同匝(單層捲繞),只需將單匝線圈的磁矩乘以匝數,就可得到總磁矩。然後,這總磁矩可以用來計算磁場,力矩,和儲存能量,方法與使用單匝線圈計算的方法相同。
假設螺線管的匝數為,每一匝線圈面積為,通過電流為,則其磁矩為
- 。
載電粒子圓周運動的磁矩
假設,一個點電荷以等速繞著z-軸,移動於半徑為的平面圓形路徑,則其電流為[7]
- 。
其磁矩為
- 。
其角動量為
- 。
其中,是載電粒子的質量。
所以,磁矩與角動量的經典關係為
- 。
對於電子,這經典關係為
- ;
其中,是電子的質量,是電子的絕對電量。
假設,這點電荷是個束縛於氫原子內部的電子。由於離心力等於庫侖吸引力,
- ;
其中,是電常數。
現在施加外磁場於此氫原子,則會有額外的勞侖茲力作用於電子。假設軌道半徑不變(這只是一個粗略計算),只有電子的速度改變為,則
- 。
所以,
- 。
假設,兩個速度的差別超小,則
- 。
所以,由於施加外磁場,磁矩的變化為
- 。
注意到與呈相反方向,因而減弱了磁場。這是抗磁性的經典解釋。可是,抗磁性是一種量子現像,經典解釋並不正確。
為了簡略計算,使用半經典方法[8],可以求出磁矩的變化為
- ;
其中,是半徑平方的期望值。
電子的磁矩
電子和許多其它種類的粒子都具有內稟磁矩。這是一種量子屬性,涉及到量子力學。詳盡細節,請參閱條目電子磁偶極矩()。微觀的內稟磁矩集聚起來,形成了巨觀的磁效應和其它物理現象,例如電子自旋共振。
電子的磁矩是
- ;
其中,是電子的朗德g因子,是波耳磁子,是電子的自旋角動量。
按照前面計算的經典結果,;但是,在狄拉克力學裏,;更準確地,由於量子電動力學效應,它的實際値稍微大些,。
請注意,由於這方程式內的負號,電子磁矩與自旋呈相反方向。對於這物理行為,經典電磁學的解釋為:假想自旋角動量是由電子繞著某旋轉軸而產生的。因為電子帶有負電荷,這旋轉所產生的電流的方向是相反的方向,這種載流迴路產生的磁矩與自旋呈相反方向。同樣的推理,帶有正電荷的正子(電子的反粒子),其磁矩與自旋呈相同方向。
原子的磁矩
在原子內部,可能會有很多個電子。多電子原子的總角動量計算,必須先將每一個電子的自旋總和,得到總自旋,再將每一個電子的軌角動量總和,得到總軌角動量,最後用角動量耦合()方法將總自旋和總軌角動量總和,即可得到原子的總角動量。原子的磁矩與總角動量的關係為[9]
- ;
其中,是原子獨特的朗德g因子。
磁矩對於磁場方向的分量是
- ;
其中,是總角動量對於磁場方向的分量,是磁量子數,可以取2J+1個整數値,-J、 -J+1、…、J-1、J,之中的任意一個整數值。
因為電子帶有負電荷,所以是負值。
處於磁場的磁偶極子的動力學,不同於處於電場的電偶極子的動力學。磁場會施加力矩於磁偶極子,迫使它依著磁場線排列。但是,力矩是角動量對於時間的導數。所以,會產生自旋進動,也就是說,自旋方向會改變。這物理行為以方程式表達為
- ;
其中,是迴轉磁比率() ,是磁場。
注意到這方程式的左手邊項目是角動量對於時間的導數,而右手邊項目是力矩。磁場又可分為兩部分:
- ;
其中,是有效磁場(外磁場加上任何自身場),是阻尼係數。
這樣,可以得到蘭道-李佛西茲-吉爾伯特方程式()[10]:
- 。
方程式右邊第一個項目描述磁偶極子繞著有效磁場的進動,第二個項目是阻尼項目,會使得進動漸漸減弱,最後消失。蘭道-李佛西茲-吉爾伯特方程式是研究磁化動力學最基本的方程式之一。
原子核的磁矩
核子系統是一種由核子(質子和中子)組成的精密物理系統。自旋是核子的量子性質之一。由於原子核的磁矩與其核子成員有關,從核磁矩的測量數據,更明確地,從核磁偶極矩的測量數據,可以研究這些量子性質。
雖然有些同位素原子核的激發態的衰變期超長,大多數常見的原子核的自然存在狀態是基態。每一個同位素原子核的能態都有一個獨特的、明顯的核磁偶極矩,其大小是一個常數,通過細心設計的實驗,可以測量至非常高的精確度。這數值對於原子核內每一個核子的獨自貢獻非常敏感。若能夠測量或預測出這數值,就可以揭示核子波函數的內涵。現今,有很多理論模型能夠預測核磁偶極矩的數值,也有很多種實驗技術能夠進行原子核測試。
分子的磁矩
任何分子都具有明確的磁矩。這磁矩可能會跟分子的能態有關。通常而言,一個分子的磁矩是下列貢獻的總和,按照典型強度從大至小列出:
參考文獻
- Jackson, John David, 3rd., USA: John Wiley & Sons, Inc.: pp. 186, 1999, ISBN 978-0-471-30932-1
- Cardarelli, F., 2nd, Springer: pp. 20–25, 2004, ISBN 1-8523-3682-X
- 美國國家標準與技術研究院(NIST)的實驗値:電子磁矩 页面存档备份,存于
- . [2010-04-10]. (原始内容存档于2009-08-22).
- Griffiths, David J., (PDF), American Journal of Physics, August 1982, 50 (8): pp. 698 [2010-04-11], (原始内容存档 (PDF)于2020-05-12)
- Boyer, Timothy H., (PDF), American Journal of Physics, 1988, 56 (8): pp. 688–692, doi:10.1119/1.15501
- Griffiths, David J., , Prentice Hall: pp. 260–262, 1998, ISBN 0-13-805326-X
- O'Dell, S. L.; Zia, R. K. P., (PDF), American Journal of Physics, Jan 1986, 54 (1): pp. 32–35
- RJD Tilley, , John Wiley and Sons: pp. 368, 2004, ISBN 0470852755
- Stuart Alan Rice, 128, Wiley: pp. 208 ff, 2004, ISBN 0471445282
