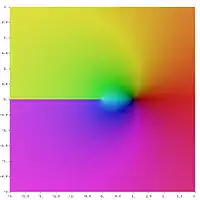
複對數

複對數（complex logarithm）為複分析中複指数函数的「反函數」，就像實數函數的自然對數ln x是指数函数e^x的反函數一様。因此复数z的对数是使以下關係式成立的複數w：e^w = z[1]。此處的w可以用log z來表示。複對數是多值函數，每個非零的複數z都有無限多個對數值[1]，因此需適當的說明，避免歧義。

複對數的一個分支。其色相表示複對數的辐角（極坐標下相對原點的角度），其顏色的飽和度及亮度表示複對數的绝对值。圖片的檔案頁中有列出其顏色對應的數值

若z = re^iθ，r > 0（極坐標），則w = ln r + iθ為z;的一個對數，而其他的對數是任一對數再加上2πi的整數倍[1]。