反三角函数
反三角函數示意圖
幾個反三角函數的圖形,其中,反餘切以複變分析定義,因此在原點處出現不連續斷點。
| 三角学 |
|---|
|
历史 三角函数 广义三角函数 反三角函数 |
| 参考 |
|
恒等式 精确值 三角表 |
| 定理 |
|
正弦定理 餘弦定理 正切定理 餘切定理 勾股定理 |
| 微积分 |
|
三角换元法 三角函数的积分 三角函数的微分 反三角函数的积分 |
數學符號
符号等常用于等。但是这种符号有时在和之间易造成混淆。
在编程中,函数, , 通常叫做, , 。很多编程语言提供两自变量atan2函数,它计算给定和的的反正切,但是值域为。
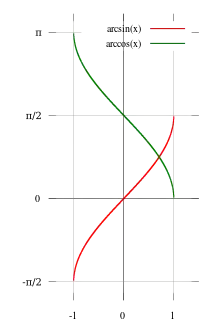 在笛卡尔平面上(紅)和(綠)函数的常用主值的图像。
在笛卡尔平面上(紅)和(綠)函数的常用主值的图像。 在笛卡尔平面上(紅)和(綠)函数的常用主值的图像。
在笛卡尔平面上(紅)和(綠)函数的常用主值的图像。 在笛卡尔平面上(紅)和(綠)函数的常用主值的图像。
在笛卡尔平面上(紅)和(綠)函数的常用主值的图像。
主值
下表列出基本的反三角函数。
| 名称 | 常用符号 | 定义 | 定义域 | 值域 |
|---|---|---|---|---|
| 反正弦 | ||||
| 反余弦 | ||||
| 反正切 | ||||
| 反余切 | ||||
| 反正割 | ||||
| 反余割 | ||||
(注意:某些數學教科書的作者將的值域定為因為當的定義域落在此區間時,的值域,如果的值域仍定為,將會造成,如果希望,那就必須將的值域定為,基於類似的理由的值域定為)
如果允许是复数,则的值域只适用它的实部。
三角函數與反三角函數的關係
通過定義可知:
| 圖示 | ||||
|---|---|---|---|---|
 | ||||
 | ||||
 | ||||
 | ||||
 | ||||
 | ||||
一般解
每个三角函数都周期于它的参数的实部上,在每个区间内通过它的所有值两次。正弦和余割的周期开始于结束于(这里的是一个整数),在到上倒过来。余弦和正割的周期开始于结束于,在到上倒过来。正切的周期开始于结束于,接着(向前)在到上重复。余切的周期开始于结束于,接着(向前)在到上重复。
这个周期性反应在一般反函数上:
反三角函数的不定积分
使用分部积分法和上面的简单导数很容易得出它们。
舉例
使用,設
則
換元
則
且
換元回x得到
加法公式和減法公式
註釋與引用
-
设,得到:
设,得到:
设,得到:
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
