冪
幂運算(英語:),又稱指數運算,是數學運算,表達式為,讀作“的次方”或「的次幂」。其中,稱為底數,而稱為指數,通常指數寫成上標,放在底數的右邊。當不能用上標時,例如在編程語言或電子郵件中,通常寫成b^n或b**n;也可視為超運算,記為b[3]n;亦可以用高德納箭號表示法,寫成b↑n。
若n為正整數, 可以把看作乘方的结果,等同於自乘次。
當指數為1時,通常不寫出來,因為運算出的值和底數的數值一樣;指數為2時,可以讀作“的平方”;指數為 3 時,可以讀作“的立方”。
起始值1(乘法的單位元)乘上底數()自乘指數()這麼多次。這樣定義了後,很易想到如何一般化指數 0 和負數的情況:除 0 外所有數的零次方都是 1 ;指數是負數時就等於重複除以底數(或底數的倒數自乘指數這麼多次),即:
- 。
0的0次方目前沒有數學家給予正式的定義。在部分數學領域中,如組合數學,常用的慣例是定義為 1 ,也有人主張定義為 1 。
因為在十进制,十的次方很易計算,只需在後面加零即可,所以科学记数法借此簡化記錄的數字;二的幂在計算機科學相當重要。
當n是複數及b是正實數時,
整数指数幂
整数指数幂的运算只需要初等代数的知识。
正整数指数幂
表达式被称作的平方,因为边长为的正方形面积是。
表达式被称作的立方,因为邊长为的正方体体积是。
所以读作3的平方,读作2的立方。
指数表示的是底数反复相乘多少次。比如,指数是5,底数是3,表示3反复相乘5次。
或者,整数指数幂可以递归地定义成:
指数是1或者0
注意表示仅仅1个3的乘积,就等于3。
注意,,,,
继续,得到,所以
另一个得到此结论的方法是:通过运算法则
当时,
- 任何数的1次方是它本身。
零的零次方
其实还并未被数学家完整的定义,但部分看法是 ,在程式语言中(python)
在这里给出这一种极限的看法
于是,可以求出 x 取值从 1 到 0.0000001 计算得到的值,如图
负数指数
我们定义任何不为 0 的数 a 的 -1 次方等于它的倒数。
对于非零定义
- ,
而时分母為 0 没有意义。
证法一:
根据定义,当时
得, 所以。
证法二:
通过运算法则
当时,可得
负数指数还可以表示成1连续除以个。比如:
- .
10的幂
在十进制的计数系统中,10的幂写成1后面跟着很多个0。例如:
因此10的幂用来表示非常大或者非常小的数字。如:299,792,458(真空中光速,单位是米每秒),可以写成 ,近似值 或 .
国际单位制词头也使用10的幂来描述特别大或者特别小的数字,比如:词头“千”就是 ,词头“毫”就是
2的幂
1的幂
1的任何次幂都为1
0的幂
0的正数幂都等于0。
0的负数幂没有定义。
任何非0之数的0次方都是1;而0的0次方是懸而未決的,某些領域下常用的慣例是約定為1。[1]但某些教科書表示0的0次方為無意義。[2]也有人主張定義為1。
负1的幂
-1的奇数幂等于-1
-1的偶数幂等于1
正实数的实数幂
一个正实数的实数幂可以通过两种方法实现。
N次方根
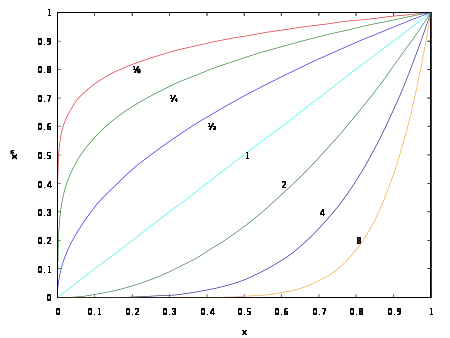
一个数的次方根是,使。
如果是一个正实数,是正整数,那么方程只有一个正实数根。 这个根被称为的次方根,记作:,其中叫做根号。或者,的次方根也可以写成. 例如
当指数是时根号上的2可以省略,如:
有理数幂
有理数指数通常可以理解成
负实数的实数幂
如果是负数且是偶数,那么是正數。如果是负数且是奇数,那么是负数。
使用对数和有理数指数都不能将(其中是负实数,实数)定义成实数。在一些特殊情况下,给出一个定义是可行的:负指数的整数指数幂是实数,有理数指数幂对于(是奇数)可以使用次方根来计算,但是因为没有实数使,对于(是偶数)时必须使用虚数单位。
使用对数的方法不能定义时的为实数。实际上,对于任何实数都是正的,所以对于负数没有意义。
使用有理数指数幂来逼近的方法也不能用于负数因为它依赖于连续性。函数对于任何正的有理数是连续的,但是对于负数,函数在有些有理数上甚至不是连续的。
例如:当,它的奇数次根等于-1。所以如果是正奇数整数,当是奇数,当是偶数。虽然有理数使的集合是稠密集,但是有理数使的集合也是。所以函数在有理数域不是连续的。
因此,如果要求负实数的任意实数幂,必须将底数和指数看成复数,按复数的正实数幂或复数的复数幂方法计算。
正实数的复数幂
e的虚数次幂
复数运算的几何意义和e的幂可以帮助我们理解(是实数),即純虛數指數函數。想象一个直角三角形(括号内是复数平面内三角形的三个顶点),对于足够大的,这个三角形可以看作一个扇形,这个扇形的中心角就等于弧度。对于所有,三角形互为相似三角形。所以当足够大时的极限是复数平面上的单位圆上弧度的点。这个点的极坐标是,直角坐标是。所以,而這個函數可以稱為純虛數指數函數。这就是欧拉公式,它通过复数的意义将代数学和三角学联系起来了。
等式的解是一个整数乘以[4]:
更一般地,如果,那么的每一个解都可以通过将的整数倍加上得到:
这个复指数函数是一个有周期的周期函数。
更简单的:。
三角函数
历史上,在复数发明之前,余弦和正弦是用几何的方法定义的。上面的公式将复杂的三角函数的求和公式转换成了简单的指数方程
使用了复数指数幂之后,很多三角学问题都能够使用代数方法解决。
e的复数指数幂
可以分解成。其中是的模,决定了的方向
正实数的复数幂
如果是一个正实数,是任何复数,定义成,其中是方程的唯一解。所以处理实数的方法同样可以用来处理复数。
例如:
复数的复数幂
复数的复数幂
类似地,在计算复数的复数幂时,我们可以将指数的实部与虚部分开以进行幂计算。例如计算:
在函數中
當函數名後有上標的數(即函數的指數),一般指要重複它的運算。例如即。特別地,指的反函數。
但三角函数的情況有所不同,一個正指數應用於函數的名字時,指答案要進行乘方運算,而指數為-1時则表示其反函數。例如:表示。因此在三角函數時,使用來表示的反函數。
计算自然数(正整数)的的算法
最快的方式计算,当是正整数的时候。它利用了测试一个数是奇数在计算机上是非常容易的,和通过简单的移所有位向右来除以2的事实。
偽代碼:
1. 1 → y, n → k, a → f
2.若k不為0,執行3至6
3.若k為奇數, y * f → y
4. k [[位操作#移位|右移]]1位(即k / 2 → k ,小數點無條件捨去)
5. f * f → f
6.回到2
7.傳回y
double power (double a, unsigned int n)
{
double y = 1;
double f = a;
unsigned int k = n;
while (k != 0) {
if (k % 2 == 1) y *= f;
k >>= 1;
f *= f;
}
return y;
}
此算法的時間複雜度為,比普通算法快(a自乘100次,時間複雜度為),在較大的時候更為顯著。
例如計算,普通算法需要算100次,上述算法則只需要算7次。若要計算可先以上述算法計算,再作倒數。
註釋
- Augustin-Louis Cauchy, Cours d'Analyse de l'École Royale Polytechnique (1821). In his Oeuvres Complètes, series 2, volume 3.
- 康軒國中1上《FUN學練功坊①》P.35:a的0次方=1(a≠0)(註:0的0次方為無意義)
- Denlinger, Charles G. . Jones and Bartlett. 2011: 278–283. ISBN 978-0-7637-7947-4.
- This definition of a principal root of unity can be found in:
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. second. MIT Press. 2001. ISBN 0-262-03293-7. Online resource 页面存档备份,存于
- Paul Cull, Mary Flahive, and Robby Robson. Undergraduate Texts in Mathematics. Springer. 2005. ISBN 0-387-23234-6. Defined on page 351, available on Google books.
- "Principal root of unity 页面存档备份,存于", MathWorld.


