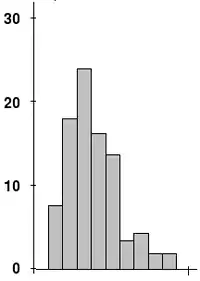
偏度
偏度(Skewness),亦稱歪度,在機率論和統計學中衡量實數隨機變量概率分布的不對稱性。偏度的值可以為正,可以為負或者甚至是無法定義。在數量上,偏度為負(負偏態;左偏)就意味着在概率密度函數左側的尾部比右側的長,絕大多數的值(不一定包括中位數在內[1])位於平均值的右側。偏度為正(正偏態;右偏)就意味着在概率密度函數右側的尾部比左側的長,絕大多數的值(不一定包括中位數[1])位於平均值的左側。偏度為零就表示數值相對均勻地分布在平均值的兩側,但不一定意味着其為對稱分布。
.svg.png.webp)
負偏態(左)和正偏態(右)
介紹
偏度分為兩種:
如果分布對稱,那麼平均值=中位數,偏度為零(此外,如果分布為單峰分布,那麽平均值=中位數=眾數)。
定義
隨機變量X的偏度γ1為三階標準矩,可被定義為:
其中μ3是三階主動差,σ是標準差。E是期望算子。等式的最後以三階累積量與二階累積量的1.5次方的比率來表示偏度。這和用四階累積量除去二階累積量的平方來表示峰度的方法向類似。
偏度有時用Skew[X]來表示。老教科書過去常常用,來表示偏度,可是由於偏度可為負,這樣的表示法較為不便。
對上面的等式進行擴展可導出用非中心矩E[X3]來表示偏度的公式:
樣本偏度
具有n個值的樣本的樣本偏度為:
其中是樣本平均值,m3是三階樣本中心矩,m2是二階樣本中心距,即樣本方差。
性質
當: 時,偏度可以是無窮大的。
或者當: (x為負)及
(x為正)時,偏度無法定義。
在後面的這個例子中,三階累積量是無法定義的。 其他分布形式比如:
二階和三階累積量是無窮大的,所以偏度也是無法定義的。
如果假定Y為n個獨立變量之和並且這些變量和X具有相同的分布,那麽Y的三階累積量是X的n倍,Y的二階累積量也是X的n倍,所以: 。根據中心极限定理,當其接近高斯分布時變量之和的偏度減小。
參考資料
- Groeneveld, RA; Meeden, G. . The Statistician. 1984, 33 (4): 391–399 [2010-10-30]. doi:10.2307/2987742. (原始内容存档于2020-08-20).
- Johnson, NL, Kotz, S, Balakrishnan N (1994) Continuous Univariate Distributions, Vol 1, 2nd Edition Wiley ISBN 0-471-58495-9
- MacGillivray, HL. . Comm. Statistics - Theory and Methods. 1992, 21: 1244–1250.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.