帳塔

在幾何學中，，又稱，是一種多面體，是透過接和兩個平行的多邊形面，一面作為頂面，另一個邊數是前者的兩倍之多邊形做為底面，然後側面由四邊形和三角形接合所產生的多面體稱為帳塔。

帳塔
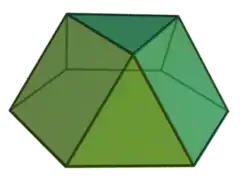
以五角帳塔為例
類別	帳塔
面	2n + 2
邊	5n
頂點	3n
歐拉特徵數	F=2n + 2, E=5n, V=3n (χ=2)
面的種類	n邊形 2n邊形 三角形 四邊形
對稱群	Cnv, [1,n], (*nn), order 2n
對偶	半偏方面體錐
旋轉對稱群	Cn, [1,n]+, (nn), order n
特性	凸

若一帳塔的面都是正多邊形，那該帳塔就屬於詹森多面體。

已知屬於詹森多面體的帳塔有：正三角帳塔、正四角帳塔、正五角帳塔，但是沒有正六角帳塔，因為正六角帳塔若每個面都是正多邊形，它將會變成一個平面。

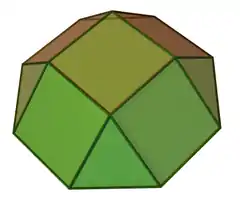
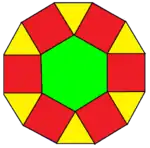
所有屬於詹森多面體的帳塔的都可以由半正多面體切去一塊得到，例如正三角帳塔是由截半立方體對切得來、正四角帳塔是由小斜方截半立方體切去中間的正八角柱而得來、正五角帳塔是由小斜方截半二十面體切去中間部份得來，另外，雖然正六角帳塔不是詹森多面體，但因他是平面，所它可以從小斜方截半六邊形鑲嵌中得來。

邊數在6邊以上的帳塔，側面不可能是正多邊形，例如正七角帳塔，除了底面是正十四邊形、頂面是正七邊形之外，側面由長方形和等腰三角形組成，因為如果是正多邊形，將無法構成多面體。

一個帳塔個以視為柱體的側面向中心對稱軸倒塌至部分頂點重和。

帳塔是擬柱體的一個子類別。