截角四面體
在幾何學中,截角四面體是一種半正八面體,13種阿基米德立體之一,共有8個面、18個邊和12個頂點,是三角化四面體的對偶多面體,可由四面體經過適當的截角,截去四面體的四個頂點所產生的多面體。
| 截角四面體 | |
|---|---|
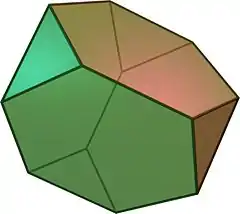 (按這裡觀看旋轉模型) | |
| 類別 | 半正多面體 |
| 面 | 8 |
| 邊 | 18 |
| 頂點 | 12 |
| 歐拉特徵數 | F=8, E=18, V=12 (χ=2) |
| 面的種類 | 正三角形 正六邊形 |
| 面的佈局 | 4{3}+4{6} |
| 頂點圖 | 3.6.6 |
| 考克斯特符號 | |
| 施萊夫利符號 | t{3,3} |
| 威佐夫符號 | 3 |
| 康威表示法 | tT |
| 對稱群 | Td群 |
| 參考索引 | U02, C16, W6 |
| 對偶 | 三角化四面體 |
| 特性 | - |
 |
 3.6.6 (頂點圖) |
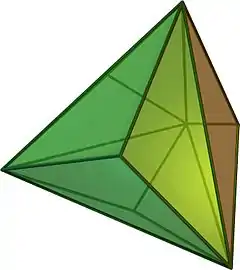 三角化四面體 (對偶多面體) |
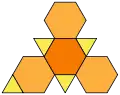 (展開圖) |
若進行更深的截角,甚至截到了中點,則稱為截半四面體,然而此種多面體與正八面體是等價的[1]。
由於截角四面體具有六邊形與三角形的面,因此也是一種戈德堡多面體,其戈德堡符號計為GIII(1,1)。
此外,由於截角四面體可以由立方體透過斜截變換構成,即先交錯、再截角,因此,截角四面體又稱為斜截立方體或截角交錯立方體,在考克斯特符號中計為![]()
![]()
![]()
![]()
![]() ,頂點數為小斜方截半立方體
,頂點數為小斜方截半立方體![]()
![]()
![]()
![]()
![]() 的一半,因此兩個截角四面體可以構成一個凸包為小斜方截半立方體的截角星形八面體,此種立體也稱為二複合截角四面體。[2]
的一半,因此兩個截角四面體可以構成一個凸包為小斜方截半立方體的截角星形八面體,此種立體也稱為二複合截角四面體。[2]
性質
截角四面體是半正多面體之一,由4個等邊三角形和4個正六邊形組成,有12個頂點和18條棱,可以想象為將正四面體的頂點切去。
座標
在直角坐標系中,將幾何中心位於原點邊長為的四面體截角產生了12個頂點,以(±3, ±1, ±1),(±1, ±3, ±1),(±1, ±1, ±3) (其中每組坐標的±數目都是奇數個)為頂點,構成了一個截角四面體。12個頂點位置如下:
- (+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
- (−3,−1,+1), (−1,−3,+1), (−1,−1,+3)
- (−3,+1,−1), (−1,+3,−1), (−1,+1,−3)
- (+3,−1,−1), (+1,−3,−1), (+1,−1,−3)
 |
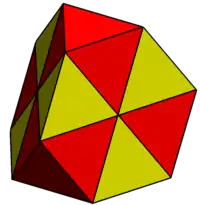 |
 |
| 正交投影顯示截角四面體可置於一個(±3,±3,±3)的邊框內。 | 截角四面體的六邊形面可分割為6共面的正三角形。其產生了四個新頂點 : (-1,-1,-1), (-1,+1,+1), (+1,-1,+1), (+1,+1,-1). |
頂點(±1,±1,±3)的全排列產生了兩個互補的截角四面體,可將之結合成一個複合多面體,即截角星形八面體。 |
交角
- 三角形與六邊形的交角:,約為109.47122063449069136924599933996°
- 六邊形與六邊形的交角:,約為70.528779365509308630754000660038°
- 兩個六邊形的共線與三角形的交角:,約為125.26438968275465431537700033002°
正交投影
| 中心 | 標準邊 | 標準面 | 邊 | 面/頂點 |
|---|---|---|---|---|
| 圖像 |  |
 |
 |
 |
| 對偶圖像 |  |
 |
 |
 |
| 投影 對稱群 |
[1] | [1] | [3] | [4] |
相關多面體及鑲嵌
| 对称性: [3,3], (*332) | [3,3]+, (332) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 | |||
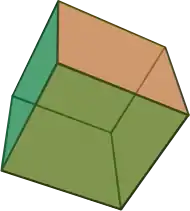
| {3,3} | t0,1{3,3} | t1{3,3} | t1,2{3,3} | t2{3,3} | t0,2{3,3} | t0,1,2{3,3} | s{3,3} |
| 半正多面体对偶 | |||||||
 |
 |
 |
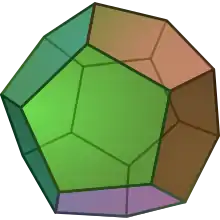 | ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
軌形對稱
 |
軌形 *n32 |
球面鑲嵌 | 歐氏鑲嵌 | 雙曲鑲嵌 | 仿緊 | ||
|---|---|---|---|---|---|---|---|
| *332 | *333 | *433 | *533 | *633... | *∞33 | ||
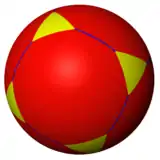
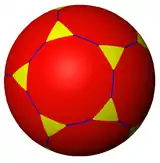
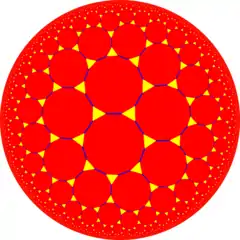
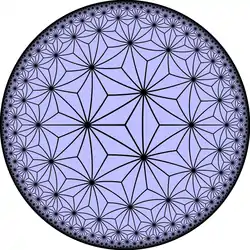
| 斜截鑲嵌 |  |
 |
 |
 |
 |
 | |
| 頂點 | 3.6.2.6 | 3.6.3.6 | 3.6.4.6 | 3.6.5.6 | 3.6.6.6 | 3.6.∞.6 | |
截角四面體圖
| 截角四面體圖 | |
|---|---|
 3倍對稱 | |
| 顶点 | 12[4] |
| 边 | 18 |
| 半径 | 3 |
| 直径 | 3[4] |
| 围长 | 3[4] |
| 自同构群 | 24 (S4)[4] |
| 色数 | 3[4] |
| 色指数 | 3[4] |
| 属性 | Hamiltonian, regular, 3-vertex-connected, planar graph |
在圖論的數學領域中,與截角四面體相關的圖為截角四面體圖,其與截角四面體有相同的拓樸結構,是一種阿基米德圖[5][6],其頂點與邊的數量及結構都與阿基米德立體中的截角四面體相同,具有12個頂點和18個邊[7]。屬於連結立體圖(英語:)[8],也是一種連結立體可遞的圖[9]。
| 圓 | 正交投影 | |
|---|---|---|
 |
 4倍對稱 |
 3倍對稱 |
參考文獻
- Chisholm, Matt; Avnet, Jeremy. . theory.org. 1997 [2013-09-02]. (原始内容存档于2014-07-21).
- Williams, Robert. . Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- 埃里克·韦斯坦因. . MathWorld.
- An Atlas of Graphs, page=172, C105
- Read, R. C.; Wilson, R. J., , Oxford University Press, 1998
- 埃里克·韦斯坦因. . MathWorld.
- An Atlas of Graphs, page=267, truncated tetrahedral graph
- An Atlas of Graphs, page=130, connected cubic graphs, 12 vertices, C105
- An Atlas of Graphs, page=161, connected cubic transitive graphs, 12 vertices, Ct11
外部連結
- 埃里克·韦斯坦因, 截角四面體 (參閱阿基米德立體) 於MathWorld(英文)
- Richard Klitzing, 3D convex uniform polyhedra, x3x3o - tut
- Editable printable net of a truncated tetrahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.