12

• 第6個合數，正因數有1、2、3、4、6和12。前一個為10、下一個為14。

  質因數分解為${\displaystyle 2^{2}\times 3}$。

• 第1個過剩數，真因數和為16，盈度為4。下一個為18。
  • 第2個半完全數，和為本身的其中一組因數為1、 2、 3、 6。前一個為6、下一個為18。
• 第5個高合成數。前一個為6、下一個為24。
• 第1個佩服數，相減後為本身的因數為2。下一個為20。
• 第4個普洛尼克數，為3與4的乘積。前一個為6、下一個為20。
• 第4個佩爾數。前一個為5、下一個為29。
• 第11個十进制的哈沙德數。前一個為10、下一個為18。
  • 除了八進制以外的進制中均為哈沙德數。
• 第5個十进制的奢侈數。前一個為9、下一個為18。
• 正十二邊形為第7個可作圖多邊形。前一個為10、下一個為15。

一个由正五边形构成的正十二面體

• 第五個不含1和2的所有因數減一都是質數的數字，前一個是8，下一個是24[1]。
• 第一組勾股数的和（埃及三角形的周长：3:4:5）
• 第三个五邊形數與有形數
• 最小的數n，使得n和n!都可表示為多個質數階乘的積（${\displaystyle 12=2!3!}$; ${\displaystyle 12!=2!3!11!}$）
• 第一個使得n ± 1、n/2 ± 1及n/3 ± 1均為質數的數，下一個這樣的數是540540
• 第三個超级階乘，即前三个阶乘的积（${\displaystyle 1!\times 2!\times 3!}$）
• 十二进制記數法的基数。以小數表示份額方面，十二进制被认为比較簡便，但是日常生活計算不會使用
• 在以13或以上的數为基数的記數法中（例如十六进制等），12以拉丁字母C標示
• 任何一對孪生素数（除了第一對外）之和的因數。
• 第一个卓越數，因為12的正因數數目（6）是個完美數，而它所有正因數之和亦是一個完美數（${\displaystyle {{{{{{1}+{2}}+{3}}+{4}}+{6}}+{12}}=28}$）。有這樣性質的數暫時只找到兩個。（OEIS中的数列A081357）
• 八皇后問題共有12個獨立解。[2][3]

基本运算

乘法	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15	16	17	18	19	20		21	22	23	24	25		50	100
${\displaystyle {{12}\times {x}}}$	12	24	36	48	60	72	84	96	108	120		132	144	156	168	180	192	204	216	228	240		252	264	276	288	300		600	1200

乘方	1	2	3	4	5	6	7	8	9	10		11
${\displaystyle {{12}^{x}}}$	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}		{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}
${\displaystyle {{x}^{12}}}$	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}	{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}		{{Ifexist not redirect{{!}}{{{數字}}}{{!}}[[{{{數字}}}]]{{!}}{{{數字}}}}}

12个小时一圈的挂钟

地球圍繞太陽公转的週期（1年；12個月），大约是月球繞地球公转週期的12倍（約1個月，陰歷定月的基礎），因此12这个数对人類的計時和曆法具有特殊的意义。

为了标示太阳每个月在黃道上的位置，古巴比伦人把每个月太阳经过的天区划分为12个星座，即黃道十二宮，十二宫（即12星座）代表了十二個基本人格型態或感情特質[4]。中国古代对周天黃道划分为十二辰和十二次。

中国古代為紀錄時間、順序等，設有12地支，排第12位的是亥。10天干配以12地支循環使用，是中國古代歷年方法，60年為一週期。每個地支再配以12种动物成為十二生肖，第12个生肖是猪。1年分為二十四節氣，配以12地支。每日计时也用地支表示，因此一天有12个时辰，由子時開始，相當於前一天23:00至當天01:00。

現代國際通用的西曆，則將1年分成12个月。12个月每月長度不一，但都有12日，分別為1月12日、2月12日、3月12日、4月12日、5月12日、6月12日、7月12日、8月12日、9月12日、10月12日、11月12日和12月12日。

1天再分成24小时，上午和下午各佔12小时。一天之內，鐘錶的时针會在以12小时划分的錶盤上转两圈，分針長度略等於時針的1.5倍，运行速度是时针的12倍。

此外，在公曆紀年方面，人類對公元前12年、公元12年，公元前12世纪及公元12世纪均有記載。

在日常生活中，12是常見的算數或貨物包裝单位，稱為一打。雞蛋、筆芯、蛋撻等都常以一打裝購買。根據《現代漢語詞典》，12打称为一簍，但這種稱謂比較少見。

在国际单位制词头中，10¹² 依据《中华人民共和国法定计量单位》称作太；依據中華民國經濟部公告的《法定度量衡單位及其使用之倍數、分數之名稱、定義及代號》称作兆（英文代号T）。10^-12 称作皮（英文代号p）。

• 在英制单位裡，1英尺的長度等於12英寸
• 中國戰國時代至隋朝使用重量单位中，十二铢等于半両
• 買賣貴金屬使用的金衡制（和称量药物的药衡制）中，12金衡制盎司（药衡制盎司）等於1金衡制磅（药衡制磅）（這和一般英制單位（常衡）中的1磅不同）
• 英国在1971年货币制度改革前，1先令等於12便士

• 量度風力的蒲福氏風級最高為12级，称作颶風[5]
• 量度地震对地面造成破坏程度的麥加利地震烈度，最高為12度[6]

鎂位于元素周期表中的第12位

• 鎂的原子序數是12[7]
• 碳的原子量为12
• 化學有十二碳雙酸（dodecanedioic acid，略作DDAD）。
• 計算物质的量使用的單位摩尔，定義就是12克碳12中所含原子數量
• 根據粒子物理学中的标准模型理论：
  • 包括反粒子在内的輕子共有12种：${\displaystyle e^{-}/e^{+},\nu _{e}/{\overline {\nu }}_{e},\mu ^{-}/\mu ^{+},\nu _{\mu }/{\overline {\nu }}_{\mu },\tau ^{-}/\tau ^{+},\nu _{\tau }/{\overline {\nu }}_{\tau }}$
  • 包括反粒子在内的夸克也有12种：${\displaystyle u/{\overline {u}},d/{\overline {d}},s/{\overline {s}},c/{\overline {c}},b/{\overline {b}},t/{\overline {t}}}$
  • 規範玻色子有12種，包括光子、3種弱相互作用的媒介粒子（${\displaystyle W^{\pm },Z\,\!}$）和8種膠子
• 位于蛇夫座的梅西耶天體M12是一个星等8.0的球状星团
• 位于双鱼座的NGC天体NGC 12是一个星等13.1的螺旋星云

列奥纳多·达·芬奇的作品《最后的晚餐》，表现了耶稣及其12个弟子

• 在希腊神话中
  • 进入万神殿的十二主神，称为“奧林匹斯十二主神”。由於不同時期有不同的神被列入十二主神之內，實際上享有這榮譽的神有14位
  • 传说曾统治世界的巨人族提坦有12位，他们是乌拉诺斯和大地女神盖娅的子女
  • 希腊神话中最伟大的英雄之一海格力斯完成了12项英雄伟绩
• 根據關於英格兰中關於亚瑟王的傳說，他有12位圆桌骑士
• 在基督教中
  • 耶稣的12个弟子称为耶稣十二门徒
  • 根据《聖經·创世纪》49·28的记载，雅各的12个儿子建立了以色列
  • 传统上，圣诞节后的第12个夜晚是主显节前夕（又叫做第十二夜），即公历的1月5日；1月6日称为顯現日（又叫做第十二日）
  • 十二大瞻礼日是东正教非常重要的一个基督教节日

• 在传统的犹太教习俗中，女孩到了12岁要举行成人礼

• 佛教中
  • 对于轮回的解释称作十二因缘论
  • 十二处是佛教中的一个常见名数
  • 佛教中还有一些12个神祇并称的名号，如藥師佛有十二神將护法，另外还有称作十二天的12个护法神
  • 《十二門論》是一部佛教典籍，內容分十二門解釋大乘空觀
  • 佛教將三藏依體裁和內容分成十二類，稱為十二分教或十二部經

• 伊斯兰教什叶派的一个分支叫做十二伊玛目派

• 道教经书的分类法中三洞四辅十二类的十二部分类法
• 摩尼教中有十二常住宝光王的名号

以色列Beit Alpha的6世纪壁画。黄道十二星座围绕着太阳，四角上的图案代表分至四时。

• 十二铜表法是罗马历史上的第一部成文法典
• 日本聖德太子定下了冠位十二階
• 日本平安时代贵族女性的一种装束称为十二单
• 10世纪中叶安南地区（今越南北部和中部部分地区）12个大封建主割地称雄，互相混战，史称十二使君之乱
• 1524－1525年发生的德国农民战争中，施瓦本北部农军在1525年3月初制定的《十二条款》
• 1991年12月9－10日，12個原歐洲共同體成員國簽訂《歐洲聯盟條約》
• 台湾於1994年提出十二項建設[8]

• 中國古代歷史
  • 中国古代將女孩12岁称為「金钗之年」
  • 周代天子冕上有十二旒，即是帽子上吊下來的穿玉絲繩，按諸侯等級旒的數目會遞減
  • 《尚書·益稷》中記載了十二章服圖，說明皇帝冕服上装饰的12种纹样；分别是元衣（外衣）上的日、月、星辰、山、龍、華蟲，黃裳上刺繡的水藻、宗彝、火、粉米、黼（音釜）、黻（音彿）
  • 前221年，秦朝統治者秦始皇下令收集全國兵器，銷毀並鑄成「十二金人（或称为十二铜人）」
  • 根據《宋史·三六五·岳飛傳》，宋朝宋高宗在一日內發出十二金牌，召回正與金作戰的岳飛回京

电话键盘

• 电脑的键盘上有12个功能键（F1、F2、F3、F4、F5、F6、F7、F8、F9、F10、F11、F12）。
• 标准的数字电话有12个拨号键（1、2、3、4、5、6、7、8、9、0、*、#）。
• 电脑換頁鍵的ASCII和Unicode碼是12。

• 汽车、蓄电池和许多弱电设备上最常见的电压是12伏特。

• 中国战国初期以漳水为源的大型引水灌溉系统是引漳十二渠。

另外一些产品的代号上也经常会看到12这个数。例如美國海軍在1980年代提出的的“先进战术攻击机”（ATA）计划的原型机A-12攻击机、哈尔滨飞机制造公司生产的运-12运输机、路易吉·弗蘭基在1979年至2000年期間生產的弗蘭基SPAS-12戰鬥霰彈槍、伊茨瑪希工廠生產的Saiga-12半自動霰彈槍以及現在由大宇集團生產的USAS-12霰彈槍。

多數的人体內有12对肋骨

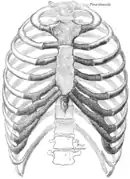
生理上，大部分的人有12对肋骨。从胃的幽门开始的小肠的起始段叫作十二指肠，相關的病症為十二指腸炎和十二指腸潰瘍，寄生蟲有十二指腸蟲，手術稱作十二指腸切開術。

根据中医的经脉学说，人体经脉有十二正经。十二正经由四肢肘、膝以上分别出来的，循行于胸、腹及头部的支脉，称为十二经别；全身筋肉按十二经脉循行分布而划分的区域则称十二经筋；十二经脉在腕、踝关节附近部位的重要腧穴称十二原穴；体表皮肤按十二经脉的循行分布而划分的区域称十二皮部；脏腑之气结聚于胸腹部的特定腧穴称募穴，共有12个。

维生素B12是一种人体必需的维生素，人類吸收主要來自動物類食品，缺乏者可導致貧血。

许多文艺作品中都有以12命名的标题。

音乐与戏剧

钢琴键盘上的12个半音

• 十二律（十二宮），相傳為黃帝的樂官伶倫，利用竹筒長短造成發音高低不同的原理，而定出的聲律準則。
• 明朝的朱载堉发明的十二平均律。
• 八度由12个半音组成。
• 十二音技法或十二音体系是音阶的一种。
• 现代音乐流派之一的十二音音乐。
• 中国女子樂隊女子十二樂坊用中樂樂器演奏流行曲，但实际上有13个成员。
• 流行于中国新疆维吾尔族地区的，以歌、舞、乐综合而成的传统古典套曲木卡姆共有12套。
• 清朝中叶昆山腔脚色行当体制中的江湖十二脚色。
• 扬剧传统剧目《十二寡妇征西》。
• 劍君十二恨是台灣布袋戲的角色之一，他的第十二恨是「天下無敵」。
• 来自于美国密歇根州底特律的说唱乐队D-12。

歐盟旗幟

青天白日旗

• L（小寫「l」）是拉丁字母的第12個字母
• Lamed是希伯來字母的第12個字母[16]
• 欧盟旗帜由12顆排成圓圈的金星組成，代表創立歐盟的12國
• 中華民國國旗等使用的青天白日圖案，太陽有12條道光芒，意念源自一天的12個時辰及一年12個月
• 足球比賽中，射点球距离球门12碼
• 根據國際法，各國領海範圍為陸地以外12海哩
• 周易的六十四卦中的第十二卦是否卦
• 英國和美國的陪审团有12人
• 黄曆中的一种曆注称为十二值
• 中国的一种传统自我推拿强身方法——十二段锦
• K-12是美国和加拿大对幼儿园（Kindergarten）至十二年级（12th grade）的简称
• 位于长江三峡的巫山十二峰
• 12岁为儿童和青少年的年龄界限

• 以「」開頭的条目
• 以「」開頭的条目

1. 《中国大百科全书·总索引》，中国大百科全书出版社，1992年 ISBN 978-7-5000-5996-7
2. Schwartzman, Steven. . Washington: Mathematical Association of America. 1994. ISBN 9780883855119.

• （英文） Why twelve — 关于数12的文章
• （英文） http://primes.utm.edu/curios/page.php/12.html页面存档备份，存于