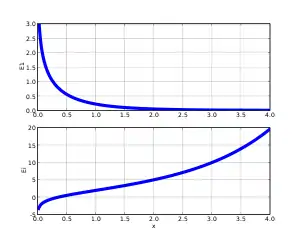
指数积分
定义
对于实数x,指数积分Ei(x)可以定义为:
其中为指数函数。以上的定义可以用于正数x,但这个积分必须用柯西主值的概念来理解。
对于自变量是复数的情形,这个定义就变得模棱两可了[1] 。为了避免歧义,我们使用以下的记法:
当自变量的实数部分为正时,可以转换为:
Ei与E1有以下关系:
性质
渐近(发散)级数
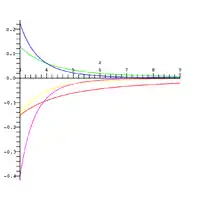
截断和中取项时,渐近展开式的相对误差
自变量的值较大时,用以上的收敛级数来计算指数积分是困难的。在这种情况下,我们可以使用发散(或渐近)级数:
这个截断和可以用来计算时函数的值。级数中的项数越多,自变量的实数部分就应该越大。
图中描述了以上估计的相对误差。
指数和对数的表现
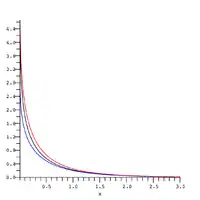
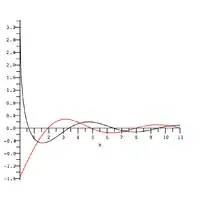
在自变量较大时的表现类似指数函数,自变量较小时类似对数函数。是位于以下两个函数之间的:
这个不等式的左端在图中用蓝色曲线来表示,中间的黑色曲线是,不等式的右端用红色曲线来表示。
参考文献
- Abramovitz, Milton; Irene Stegun. . Abramowitz and Stegun. New York: Dover. 1964. ISBN 0-486-61272-4.
- Press, William H. et al. Numerical Recipes (FORTRAN). Cambridge University Press, New York: 1989.
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 5)
- R. D. Misra, Proc. Cambridge Phil. Soc. 36, 173 (1940)
- S. Chandrasekhar, Radiative transfer, reprinted 1960, Dover
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.