比例

若存在一非零常数${\displaystyle k}$使

${\displaystyle y=kx}$

则称变量${\displaystyle y}$与变量${\displaystyle x}$成比例（有时也称为成正比）。当${\displaystyle x}$和${\displaystyle y}$成正比关系，表示当${\displaystyle x}$变为原來${\displaystyle k}$倍时，${\displaystyle y}$也会变为原來的${\displaystyle k}$倍。

• ${\displaystyle y}$是應变量
• ${\displaystyle x}$是自变量
• ${\displaystyle k}$则是变分常数，而${\displaystyle k}$不等于${\displaystyle 0}$。如${\displaystyle k=0}$，则不能成立正比关系。也就是说，${\displaystyle x,y}$两个变量成线性函数关系。

该关系通常用${\displaystyle \propto }$（U+221D）表示为：

${\displaystyle y\propto x}$

并称该常数比率

${\displaystyle k={\frac {y}{x}}}$

为比例常数或比例关系中的比例恒量。

在日常生活中，正比这个词的使用并不严格局限于线性函数，一般来说，一个变量随着另一个变量的增大／缩小而相应地增大／缩小，近似地满足线性关系的时候，我们可以说这两个变量成正比。

現代數學對於比例的用法並沒有嚴格限制，例如，在一個班級裡面，我們可以說：「男孩與女孩的比例是2比1」。然而，在古希臘數學中，由於比例是用來表示倍數關係，所以必須是相同種類的數量才能構成比例，例如，歐幾里得在《幾何原本》第五冊中如此定義比例[2]：

比例是兩個同類數量之間的大小關係。

阿基米德使用這個定義來敘述均勻運動（）的等比關係[3]：

在一個均勻運動中，兩段距離的比例相等於它們所需時間的比例。

阿基米德所要描述的，就是勻速運動，但是古希臘數學並不接受距離與時間的比例[4]（亦即速率），因為它們是不一樣的數量，所以他沒有辦法直接說：「均勻運動就是每一點上的速率皆相等」。當採用古希臘的比例論來敘述時，必須取兩段距離${\displaystyle L_{1}}$與${\displaystyle L_{2}}$以及所需時間${\displaystyle T_{1}}$與${\displaystyle T_{2}}$，均勻運動（勻速運動）就是${\displaystyle L_{1}:L_{2}=T_{1}:T_{2}}$。

• 假设某人以匀速运动，则其运动的距离是和运动的时间成正比的，所以速度就是当中的比例常数。
• 圆的周长与其直径成正比，当中的比例常数就是π。
• 在按比例尺绘制的地图上，地图上任意两点间的距离是和该两点所代表的实际地点之间的距离成比例的，当中的比例常数即是绘制该地图所使用的比例尺系数。
• 物理学中，地球的重力对在海平面上的某物体的作用力的数值与该物体的质量成正比，当中的比例常数是地球的重力加速度。

因为

${\displaystyle y=kx}$

等价于

${\displaystyle x={\frac {1}{k}}\cdot y}$

因此可推出，若 ${\displaystyle y}$ 与 ${\displaystyle x}$ 之间存在正比关系，则 ${\displaystyle x}$ 与 ${\displaystyle y}$ 之间存在正比关系。

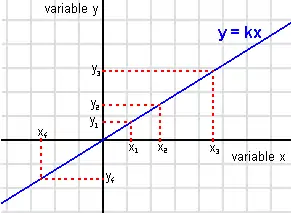
${\displaystyle y}$ 与 ${\displaystyle x}$ 的正比关系也可以被解读为一条在二维直角坐标系穿过原点的直线，其斜率为比例常数。

比例关系中，位于两端的两数之积等于位于中间的两数之积：

${\displaystyle {\frac {a}{b}}={\frac {c}{d}}\iff ad=bc}$

在上面定义中，我们说有时称两个成比例的变量成正比例，这是为了和反比例关系相对应。

如果两变量中，一个变量和另外一个变量的倒数成正比，或等价地，若这两变量的乘积是一个常数，则称这两个变量是成反比例（或相反地变化）的。从而可继续推出，若存在一非零常数${\displaystyle k}$使

${\displaystyle y={\frac {k}{x}}}$

则变量${\displaystyle y}$和变量${\displaystyle x}$成反比。

反比例关系的概念基本上说明的是这样一种关系，即当一个变量的值变大时，另一变量的值相应变小，而两者之积总是保持为一常数（即比例常数）。

举例来说，运动中的车辆走完一段路程所花费的时间是和这辆车运动的速度成反比的；在地上挖个坑所花的时间也（大致地）和雇来挖坑的人数成反比的。

在笛卡尔坐标平面上，两个具有反比例关系的变量的图形是一对双曲线。该图线上的每一点的 X 和 Y 坐标值之积总是等于比例常数${\displaystyle k}$。由于${\displaystyle k}$非零，所以图线不会与坐标轴相交

若变量${\displaystyle y}$与变量${\displaystyle x}$的指数函数成正比，即：若存在非零常数${\displaystyle k}$使

${\displaystyle y=ka^{x}}$

则称${\displaystyle y}$与${\displaystyle x}$成指数比例。

类似地，若变量${\displaystyle y}$与变量${\displaystyle x}$的对数函数成正比，即：若存在非零常数${\displaystyle k}$使

${\displaystyle y=k\log _{a}{x}}$

则称${\displaystyle y}$与${\displaystyle x}$成对数比例。

用实验方法确定两个物理量是否具有正比关系，可采用这样的办法，即进行多次测量并在笛卡尔坐标系中将这些测量结果用多个点来表示，而绘制出这些点的分布图形；如果所有点完全（或接近）地落在一条穿过原点${\displaystyle (0,0)}$的直线上，则这两个变量（很有可能）具有比例常数等于该直线斜率的正比关系。

• 比率
• 相似性
• 比例字体
• 相关性
• 三数法则
• 比例论