波函数
在量子力學裏,量子系統的量子態可以用波函數(英語:)來描述。薛丁格方程式設定波函數如何隨著時間流逝而演化。從數學角度來看,薛丁格方程式乃是一種波動方程式,因此,波函數具有類似波的性質。這說明了波函數這術語的命名原因。
波函數 是一種複值函數,表示粒子在位置 、時間 的機率幅,它的絕對值平方 是在位置 、時間 找到粒子的機率密度。以另一種角度詮釋,波函數是「在某時間、某位置發生相互作用的概率幅」。[1]
波函數的概念在量子力學裏非常基礎與重要,諸多關於量子力學詮釋像謎一樣之結果與困惑,都源自於波函數,甚至今天,這些論題仍舊尚未獲得滿意解答。
歷史


在1920年代與1930年代,理論量子物理學者大致分為兩個陣營。第一個陣營的成員主要為路易·德布羅意和埃爾溫·薛丁格等等,他們使用的數學工具是微積分,他們共同創建了波動力學。第二個陣營的成員主要為維爾納·海森堡和馬克斯·玻恩等等,使用線性代數,他們建立了矩陣力學。後來,薛丁格證明這兩種方法完全等價。[2]:606–609
德布羅意於1924年提出的德布羅意假說表明,每一種微觀粒子都具有波粒二象性。電子也不例外,具有這種性質。電子是一種波動,是電子波。電子的能量與動量分別決定了它的物質波頻率與波數。既然粒子具有波粒二象性,應該會有一種能夠正確描述這種量子特性的波動方程式,這點子給予埃爾溫·薛定諤極大的啟示,他因此開始尋找這波動方程式。薛定諤參考威廉·哈密頓先前關於牛頓力學與光學之間的類比這方面的研究,在其中隱藏了一個奧妙的發現,即在零波長極限,物理光學趨向於幾何光學;也就是說,光波的軌道趨向於明確的路徑,而這路徑遵守最小作用量原理。哈密頓認為,在零波長極限,波傳播趨向於明確的運動,但他並沒有給出一個具體方程式來描述這波動行為,而薛定諤給出了這方程式。他從哈密頓-雅可比方程成功地推導出薛定谔方程式。[3]:207他又用自己設計的方程式來計算氫原子的譜線,得到的答案與用波耳模型計算出的答案相同。他將這波動方程式與氫原子光譜分析結果,寫為一篇論文,1926年,正式發表於物理學界[4][5]:163-167。從此,量子力學有了一個嶄新的理論平台。
薛丁格給出的薛定諤方程式能夠正確地描述波函數的量子行為。那時,物理學者尚未能解釋波函數的涵義,薛定諤嘗試用波函數來代表電荷的密度,但遭到失敗。1926年,玻恩提出機率幅的概念,成功地解釋了波函數的物理意義[3]:219-220。可是,薛定諤本人不贊同這種統計或機率方法,和它所伴隨的非連續性波函數塌縮,如同愛因斯坦認為量子力學只是個決定性理論的統計近似,薛定諤永遠無法接受哥本哈根詮釋。在他有生最後一年,他寫給玻恩的一封信內,薛定諤清楚地表明了這意見。[3]:479
1927年,道格拉斯·哈特里與弗拉基米尔·福克在對於多體波函數的研究踏出了第一步,他們發展出哈特里-福克方程來近似方程的解。這計算方法最先由哈特里提出,後來福克將之加以改善,能夠符合包立不相容原理的要求。[6]:344-345
薛定谔方程式不具有勞侖茲不變性 ,无法准确给出符合相对论的结果。薛定諤試著用相對論的能量動量關係式,來尋找一個相對論性方程式,並且描述電子的相对论性量子行為。但是這方程式給出的精細結構不符合阿諾·索末菲的結果,又會給出違背量子力學的負機率和怪異的負能量現象,他只好將這相對論性部分暫時擱置一旁,先行發表前面提到的非相對論性部分。[3]:196-197[7]:3
1926年,奥斯卡·克莱因和沃尔特·戈尔登將電磁相對作用納入考量,獨立地給出薛定谔先前推導出的相對論性部分,並且證明其具有勞侖茲不變性。這方程式後來稱為克莱因-戈尔登方程式。[7]:3
1928年,保羅·狄拉克最先成功地統一了狹義相對論與量子力學,他推導出狄拉克方程式,適用於電子等等自旋為1/2的粒子。這方程式的波函數是一個旋量,擁有自旋性質。[5]:167
概述
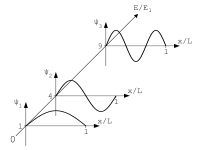
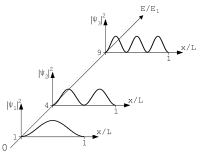
位置空間波函數
假設一個自旋為零的粒子移動於一維空間。這粒子的量子態以波函數表示為 ;其中, 是位置, 是時間。波函數是複值函數。測量粒子位置所得到的結果不是決定性的,而是機率性的。粒子的位置 在區間 (即 )的機率為
- ;
其中, 是對於粒子位置做測量的時間。
換句話說, 是粒子在位置 、時間 的機率密度。
這導致歸一化條件:在位置空間的任意位置找到粒子的機率為100%:
- 。
動量空間波函數
在動量空間,粒子的波函數表示為 ;其中, 是一維動量,值域從 至 。測量粒子動量所得到的結果不是決定性的,而是機率性的。粒子的動量 在區間 (即 )的機率為
- 。
動量空間波函數的歸一化條件也類似:
- 。
薛丁格方程式
在一維空間裏,運動於位勢 的單獨粒子,其波函数滿足含時薛丁格方程式
- ;
其中, 是質量, 是約化普朗克常數。
不含時薛丁格方程式與時間無關,可以用來計算粒子的本徵能量與其它相關的量子性質。應用分離變數法,猜想 的函數形式為
- ;
其中, 是分離常數,稍加推導可以論定 就是能量, 是對應於 的本徵函數。
代入這猜想解,經過一番運算,可以推導出一維不含時薛丁格方程式:
- 。
波函数的概率诠释
波函数 是概率波。其模的平方 代表粒子在该处出现的概率密度,并且具有归一性,全空间的积分
- 。
波函数的另一个重要特性是相干性。两个波函数叠加,概率的大小取决于两个波函数的相位差,类似光学中的杨氏双缝实验。
波函数的本征值和本征态
在量子力学中,可观察量 以算符 的形式出现。 代表对於波函数的一种运算。例如,在位置空間裏,动量算符 的形式為
- 。
可观察量 的本徵方程式為
- 。
对应的 称为算符 的本徵值, 称为算符 的本徵態。假設對於 的本徵態 再測量可观察量 ,則得到的結果是本徵值 。
态叠加原理
假設對於某量子系統測量可觀察量 ,而可觀察量 的本徵態 、 分別擁有本徵值 、 ,則根据薛定谔方程的线性关系,疊加態 也可以是這量子系統的量子態:
- ;
其中, 、 分別為疊加態處於本徵態 、 的機率幅。
假設对這疊加態系統测量可观察量 ,則測量獲得數值是 或 的機率分別為 、 ,期望值為
- 。
定态
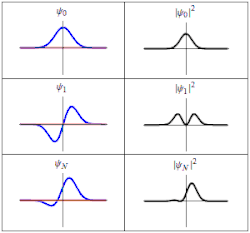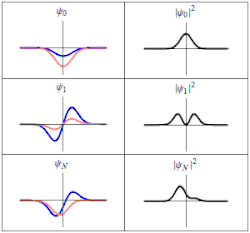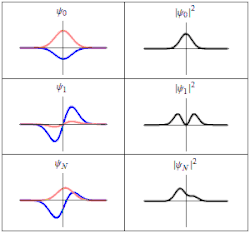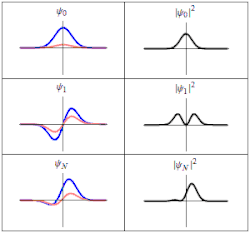
在量子力学中,一类基本的问题是哈密顿算符 不含时间的情况。對於這問題,應用分離變數法,可以將波函數 分離成一个只与位置有关的函数 和一个只与时间有关的函数 :
- 。
將這公式代入薛定谔方程,就会得到
- 。
而 则满足本徵能量薛丁格方程式:
- 。
例子
有限位势垒

在1D情况下,粒子处于如下势垒中:
其波函数的定态解为(为常数)
参考文獻
- Hobson, Art. . American Journal of Physics. 2013, 81 (211). doi:10.1119/1.4789885.
- Hanle, P.A., , Isis, December 1977, 68 (4), doi:10.1086/351880
- Moore, Walter John, , England: Cambridge University Press, 1992, ISBN 0-521-43767-9 (英语)
- 薛定諤, 埃尔温, (PDF) 79, Annalen der Physik, (Leipzig), 1926 [德文原稿]
- Kragh, Helge. illustrated, reprint. Princeton University Press. 2002. ISBN 9780691095523.
- Atkins, Peter; de Paula, Julio. 8th. W. H. Freeman. 2006. ISBN 978-0716787594.
- McMahon, David. . McGraw Hill Professional. 2008. ISBN 9780071643528.
- Griffiths, David J., , Prentice Hall, 2004, ISBN 0-13-111892-7



