維格納半圓分布
維格納半圓分布是一以物理學家尤金·維格納(Eugene Wigner)命名的機率分佈。其機率密度函數(Probability Distribution Function)係一存在[-R,R]區間內的半圓形分佈、以(0,0)為中心點並經過適當規範化(Normalized)的結果,因而其實其函數圖型是一半橢圓形。
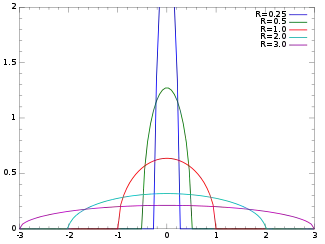 density函數 | |
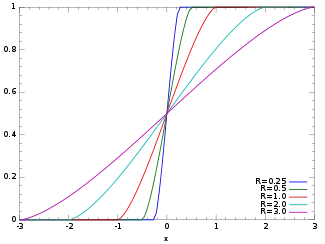 累積分布函數 | |
| radius (real) | |
| 值域 | |
| 累積分布函數 | for |
| 期望值 | |
| 中位數 | |
| 眾數 | |
| 偏度 | |
| 峰度 | |
| 熵 | |
| 特徵函数 | |
for −R ≤ x ≤ R, and f(x) = 0 if R < |x|.
此機率分佈可做為一大小接近無限的隨機對稱矩陣,其特徵值(Eigenvalues) 的分布限制範圍。
它是一個經過縮放的Β分布(Beta Distribution)。精確而言:當Y值有B分布(α = β = 3/2)時,則其X = 2RY – R值具備上述分佈特性。
性質
第二種切比雪夫多項式(Chebyshev Polynomial)是此分布的正交多項式 (Orthogonal Polynomial) 。對於正整數n,此分佈之第2n項動差(Moment)為:
此處 X是一隨機變數,而Cn是第n項 卡塔蘭數(Catalan number):
因此若R=2,此分佈之動差為卡塔蘭數。
(因為對稱性的關係,所有奇數項之動差皆為0)
若以 替代式子動差生成函數(Moment generating Function)內的x,則我們可以發現:
並得以此式子得出(詳見Abramowitz and Stegun §9.6.18):
式中的 是一變異貝索函數(Modified bessel functions)。
同樣地,其特徵方程式:
其中的 是貝索函數。( 詳見 Abramowitz and Stegun §9.1.20)。若取一有限且接近0的實數 ,則維格納半圓分布成為一狄拉克δ函数 (Dirac delta function)。微分方程式 (Differential equation)
與非古典機率的關係
在 非古典機率 (free probability) 理論中,維格納半圓分布有著如同常態分佈 (Normal Distribution) 在古典機率中一樣的角色。 也就是說,在非古典機率中,累積量 (Cumulant) 的角色被"自由累積量" (free Cumulant、待翻譯)。
參看
- The W.s.d. is the limit of the Kesten–McKay distributions, as the parameter d tends to infinity.
- In number-theoretic literature, the Wigner distribution is sometimes called the Sato–Tate distribution. See Sato–Tate conjecture.
- Marchenko–Pastur distribution or Free Poisson distribution
參考
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972.
相關連結
- Eric W. Weisstein et al., Wigner's semicircle
