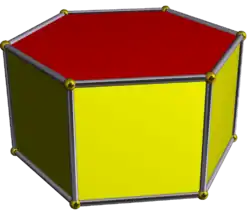
三角柱堆砌

三角柱堆砌的胞為三角柱，因此三角柱也是一種空間填充多面體[5]。

三角柱堆砌的對偶堆砌體為六角柱堆砌[6]。六角柱堆砌是一種由六角柱獨立填滿三維空間的幾何結構[7]。

六角柱堆砌
類型	堆砌
維度	3
胞	六角柱
施萊夫利符號	{6,3}×{∞} 、 t0,1,3{6,3,2,∞}
考克斯特群	[6,3,2,∞] [3[3],2,∞]
對偶多胞體	三角柱堆砌
特性	胞可遞、點可遞

六角柱堆砌是一種由六角柱獨立填滿三維空間的幾何結構[7]，其為三角柱堆砌的對偶堆砌體。[6]

六角柱堆砌的所有包皆為六角柱組成，因此其具有胞可遞的特性；其每個頂點都是6個六角柱的公共頂點[4]，因此六角柱堆砌也具有點可遞的特性。六角柱堆砌有兩種稜，一種是4個六角柱的公共稜，另一種是3個六角柱的公共稜，因此六角柱堆砌並不具有稜可遞的特性。

三角柱堆砌的胞為六角柱，因此六角柱也是一種空間填充多面體[8]。

六角柱堆砌的對偶堆砌體為三角柱堆砌。三角柱堆砌是一種由三角柱獨立填滿三維空間的幾何結構[7]。

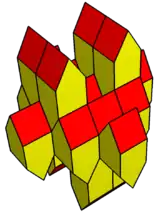
異相三角柱堆砌
類型	堆砌
維度	3
胞	三角柱
施萊夫利符號	{3,6}:g×{∞} {4,4}f{∞}
考克斯特群	[6,3,2,∞] [3[3],2,∞]
對偶多胞體	柱狀異相雙三角柱堆砌
特性	點可遞

異相三角柱堆砌是一種三角柱堆砌，其同樣由三角柱獨立堆砌而成，但其是以各三角柱底面並非全部互相平行的方式完成堆砌，其是透過三角柱兩兩一組以異相雙三角柱的組合方式為單位獨立填滿三維空間的幾何結構。由於組成異相三角柱堆砌的胞——三角柱是一種柱形均勻多面體，因此異相三角柱堆砌也可以視為一種均勻堆砌體[9]。異相三角柱堆砌的對偶堆砌體為由柱狀異相雙三角柱（扭稜鍥形體的對偶多面體）組成的堆砌體[6]。

異相雙三角柱堆砌是一種由異相雙三角柱獨立填滿三維空間的幾何結構，其頂點與異相三角柱堆砌共用的幾何結構，其可以視為將異相三角柱堆砌中每兩個可組合成異相雙三角柱的胞，兩兩一組視為同一個胞。異相雙三角柱堆砌是唯一一種由詹森多面體填滿三維空間的幾何結構[10][11][12]。

異相雙三角柱堆砌的胞為異相雙三角柱，同時，異相雙三角柱也是唯一一種能獨立填滿空間的詹森多面體[11][12]。

同相三角柱-立方體堆砌
類型	堆砌
維度	3
胞	三角柱 立方體
施萊夫利符號	{3,6}:e×{∞} s{∞}h1{∞}×{∞}
考克斯特群	[∞,2+,∞,2,∞] [(∞,2)+,∞,2,∞]
特性	點可遞

同相三角柱-立方體堆砌是一種由三角柱和立方體共同堆砌填滿空間的幾何結構，可以視為在同相三角柱堆砌與立方體堆砌分層的組合結果，是28種由均勻多面體組成的堆砌體之一[13]。

異相三角柱-立方體堆砌
類型	堆砌
維度	3
胞	三角柱 立方體
施萊夫利符號	{3,6}:ge×{∞} {4,4}f1{∞}
特性	點可遞

異相三角柱-立方體堆砌是一種由三角柱和立方體共同堆砌填滿空間的幾何結構，可以視為在異相三角柱堆砌與立方體堆砌分層的組合結果，是28種由均勻多面體組成的堆砌體之一[13]。

若將異相三角柱-立方體堆砌中，每個立方體與相鄰的三角柱、和位於該三角柱所在立方體面對面的另一個三角柱為一組視為一個柱狀異相雙三角柱（扭稜鍥形體的對偶多面體）所形成的一個純粹由柱狀異相雙三角柱填滿空間的幾何結構則為異相三角柱堆砌的對偶堆砌體[6]。