六角柱
在幾何學中,六角柱又稱六角稜柱[1],是一種底面為六邊形的柱體[2]。所有六角柱都有8個面,18個邊和12個頂點[3]。
| 正六角柱 | |
|---|---|
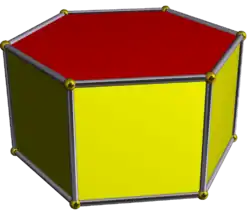 正六角柱 | |
| 類別 | 柱體 |
| 面 | 8 |
| 邊 | 18 |
| 頂點 | 12 |
| 歐拉特徵數 | F=8, E=18, V=12 (χ=2) |
| 面的種類 | 六邊形×2 正方形×6 |
| 面的佈局 | 6{4}+2{6} |
| 頂點圖 | 4.4.6 |
| 考克斯特符號 | |
| 施萊夫利符號 | t{2,6} or {6}x{} |
| 威佐夫符號 | 2 |
| 康威表示法 | P6 |
| 對稱群 | D6h, [6,2], (*622), order 24 |
| 參考索引 | U76(d) |
| 對偶 | 雙六角錐 |
| 特性 | 凸、 zonohedron |
 |
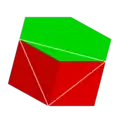 4.4.6 (頂點圖) |
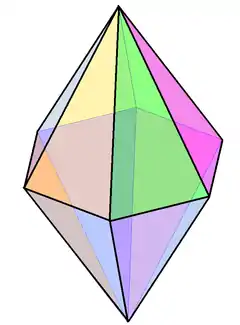 雙六角錐 (對偶多面體) |
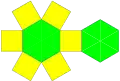 (展開圖) |
由於它具有8個面,所以它是一個八面體[4]。然而,“八面體”這個幾何術語,主要是指正八面體,其中有8個三角形面。這個若稱做八面體的話,會和正八面體混淆,所以很少使用“八面體”來表示六角柱。
許多鉛筆在削尖之前的形狀都是六角柱形[5]。
性質
正六角柱是指底面為正六邊形的六角柱,其每個頂點都是2個正方形和1個正六邊形的公共頂點,因此具有點可遞的性質,又因其所有面都是正多邊形因此是一種半正多面體,且其為以正方形為側面的半正柱體無窮系列中的第4個幾何體。六角柱亦可以視為一種截角六面形,並可以以施萊夫利符號t{2,6}表示。
對稱性
| 對稱性 | D6h, [2,6], (*622) | C6v, [6], (*66) | D3h, [2,3], (*322) | D3d, [2+,6], (2*3) | |
|---|---|---|---|---|---|
| 結構 | {6}×{}, |
t{3}×{}, |
s2{2,6}, | ||
| 圖像 |  |
 |
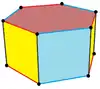 |
 | |
| 扭曲 | 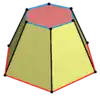 |
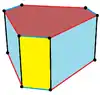 |
  |
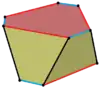 | |
構成多胞形
六角柱可以獨立堆砌成堆砌體,也可以跟其他立體共同堆砌密鋪三維空間
| 六角柱堆砌[3] |
三角柱-六角柱堆砌 |
扭稜六邊形鑲嵌柱堆砌 |
大斜方截半六邊形鑲嵌柱堆砌 |
 |
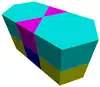 |
 |
 |
| 截角四面體柱體 |
截角八面體柱體 |
大斜方截半立方體柱體 |
截角二十面體柱體 |
大斜方截半二十面體柱體 |
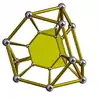 |
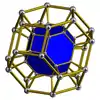 |
 |
 |
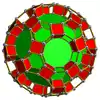 |
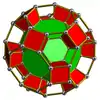
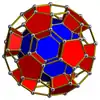
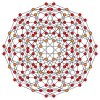
| 柱形斜方截半正五胞體 |
大柱形斜方截半正五胞體 |
柱形斜方截半正十六胞體 |
大柱形斜方截半超立方體 | |
 |
 |
 |
 | |
| 柱形斜方截半正二十四胞體 |
大柱形斜方截半正二十四胞體 |
柱形斜方截半正六百胞體 |
大柱形斜方截半正一百二十胞體 | |
 |
 |
 |
 |
相關多面體與鑲嵌
| 對稱群:[6,2], (*622) | [6,2]+, (622) | [1+,6,2], (322) | [6,2+], (2*3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 | ||
| {6,2} | t{6,2} | r{6,2} | 2t{6,2}=t{2,6} | 2r{6,2}={2,6} | rr{6,2} | tr{6,2} | sr{6,2} | h{6,2} | s{2,6} |
| 半正對偶 | |||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V32 | V3.3.3.3 |
大斜方截半變異對稱性
| *n32的大斜方截半變異對稱性: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 對稱性 *n32 [n,3] |
球面 | 平面 | 緊湊雙曲 | 仿緊 | 非緊雙曲 | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| 圖形 |  |
 |
 |
 |
 |
 |
 |
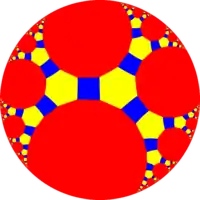 |
 |
 |
 | |
| 頂點布局 | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| 對偶 |  |
 |
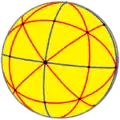 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 面布局 | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
參考文獻
- . 國家教育研究院. [2016-08-17]. (原始内容存档于2016-08-17).
- . Maths A to Z. School A to Z. [2016-08-17]. (原始内容存档于2016-08-17).
- Pugh, Anthony, , University of California Press: 21, 27, 62, 1976 [2014-06-22], ISBN 9780520030565, (原始内容存档于2014-07-09).
- 埃里克·韦斯坦因. . MathWorld.
- Simpson, Audrey, , Cambridge University Press: 266–267, 2011 [2016-08-03], ISBN 9780521727921, (原始内容存档于2020-11-02).
- Jim Reed. . 埃德蒙頓公立學校. 1998年7月 [2016-02-23]. (原始内容存档于2009-11-04).
- . 里賈納大學. [2016-08-17]. (原始内容存档于2015-09-23).
- . eusebeia. 2014-02-28 [2016-08-17]. (原始内容存档于2014-03-02).
外部連結
- Hexagonal Prism Interactive Model -- works in your web browser
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.