二面體

在幾何學中，二面體是指由2個面組成的多面體，但由於三維空間中的多面體至少又具有4個面，因此少於四個面的多面體只能是退化的，換句話說，小於4個面的多面體無法具有非零的體積。二面體中最常見的就是多邊形二面體，即由兩個全等的平面圖型封閉出的零體積空間所形成的退化多面體。最簡單的二面體是一種球面鑲嵌：一角形二面體，它的對偶是一面形。

部分的二面體

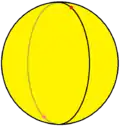二面形
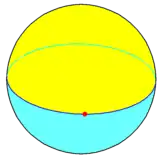一角形二面體

常見的二面體
名稱 種類 圖像 符號 頂點 邊 面 χ 面的種類 對稱性
一角形二面體 多邊形二面體 {1,2}
 1 1 2 2 2個一角形 C1v
（*22）
二面形 多面形
多邊形二面體		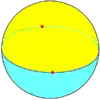 {2,2}
 2 2 2 2 2個二角形 D2h
（*222）
三維多邊形 多邊形二面體 {n,2}
 n n 2 2 2個全等的多邊形 Dnh
（*n22）
二階無限邊形鑲嵌[2] 鑲嵌圖 {∞,2}

 ∞ ∞ 2 2 2個無限邊形 [∞,2], (*∞22)
{4,4}1,1 環形多面體 {4,4}1,1 2 4 2 0 2個正方形
{3,6}1,0 環形多面體 {3,6}1,0 1 3 2 0 2個正三角形
圓錐體 非嚴格多面體
曲面
柱體		 1 1 2 2 1個曲面
1個圓形

平面圖形
主条目：多邊形二面體

任何平面圖形都可以視為一個二面體，並且屬於二面體群。

若將一封閉的平面圖形放置於三維空間也可以視為一個二面體，如多邊形二面體。他們皆屬於二面體群，是透鏡空間的基本域[3]。

球面鑲嵌

二面體可以以球面鑲嵌的方式存在，最簡單的例子是二面形。

名稱 二面形 一角形二面體 多邊形二面體
圖像
施萊夫利符號 {2,2} {1,2}
h{2,2}		 {n,2}
考克斯特記號

二面形
主条目：多面形

一個二面形，是一種由二個鑲嵌在球體上的球弓形組成的多面形，施萊夫利符號中利用{2,2}來表示，該符號表達了二面形的結構——每個頂點都是2個二角形的公共頂點。

一角形二面體

一角形二面體是一種退化的多邊形二面體，由2個一角形組成，圖形只有1個頂點，該頂點為2個一角形的公共頂點，在施萊夫利符號中用{1,2}表示，其具有2個面、1條邊和1個頂點，對偶多面體是一個一面體：一面形。

在球面幾何學中，一角形二面體是一個球面上的一個圓上任一頂點。這形成了一個二面體，施萊夫利符號中利用{1,2}來表示，與的兩個半球形一角形面，共用一個360°的邊和一個頂點。它的對偶是一面形，施萊夫利符號中利用{2,1}來表示，具有一個二角形面（一個完整的360°弓形），一個180°的邊緣，和兩個頂點，因此屬於一面體。

圓錐

圓錐也能算是一種二面體，因為它可以看做是只有兩個面的幾何體，由一曲面(側面)和一圓形平面(底面)所組成。

參見

參考文獻
  1. The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
  2. Conway (2008)[1], p. 263
  3. Gausmann, Evelise; Roland Lehoucq, Jean-Pierre Luminet, Jean-Philippe Uzan, Jeffrey Weeks. . Classical and Quantum Gravity. 2001, 18: 5155–5186. arXiv:gr-qc/0106033. doi:10.1088/0264-9381/18/23/311.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.