密度矩陣
在量子力學裏,密度算符(英語:)與其對應的密度矩陣(英語:)專門描述混合態量子系統的物理性質。純態是一種可以直接用態向量 來描述的量子態,混合態則是由幾種純態依照統計機率組成的量子態。假設一個量子系統處於純態 、 、 、……的機率分別為 、 、 、……,則這混合態量子系統的密度算符 為
- 。
注意到所有機率的總和為1:
- 。
假設 是一組規範正交基,則對應於密度算符的密度矩陣 ,其每一個元素 為
- 。
- ,
是可觀察量 對於每一個純態的期望值 乘以其權值 後的總和。
混合態量子系統出現的案例包括,處於熱力學平衡或化學平衡的系統、製備歷史不確定或隨機變化的系統(因此不知道到底系統處於哪個純態)。假設量子系統處於由幾個糾纏在一起的子系統所組成的純態,則雖然整個系統處於純態,每一個子系統仍舊可能處於混合態。在量子退相干理論裏,密度算符是重要理論工具。
密度算符是一種線性算符,是自伴算符、非負算符(英語:)、跡數為1的算符。關於密度算符的數學形式論是由約翰·馮·諾伊曼與列夫·郎道各自獨立於1927年給出。[1][2]:48-55[3]
純態與混合態
假設一個量子系統的量子態是純態,則這量子態可以用態向量表示為 。幾種純態依照機率組成的量子態稱為混合態。例如,假設一個量子系統處於純態 、 的機率都為50%,則這量子系統處於混合態。密度矩陣專門用來表示混合態。任何量子態,不管是純態,還是混合態,都可以用密度矩陣表示。
混合態與疊加態的概念不同,幾種純態通過量子疊加所組成的疊加態仍舊是純態。例如, 是個純態。
光子偏振案例


光子的兩種圓偏振態,右旋圓偏振態與左旋圓偏振態,分別以態向量 、 標記。光子也可能處於疊加態,例如,垂直偏振態與水平偏振態分別為 、 。更一般地,光子偏振所處於的疊加態可以表示為 ;其中, 、 是係數。這一般式可以表示平面偏振態、圓偏振態、橢圓偏振態等等。
假若讓處於疊加態 的光子通過左旋圓偏振器,則出射的光子處於左旋圓偏振態 ;假若通過右旋圓偏振器,則出射的光子處於右旋圓偏振態 。對於這兩種圓偏振模,光子強度都會減半,貌似意味著疊加態 的一半光子處於量子態 ,另一半處於量子態 ,但這種解釋並不正確,處於量子態 與 的光子都有可能被垂直平面偏振器吸收,但是處於量子態 的光子不會被垂直平面偏振器吸收。
從白熾燈發射出的光子是一種非偏振態光子,不能用疊加態 來描述。特別而言,與平面偏振態光子不同,它通過任何偏振器後都會失去50%強度,與圓偏振態光子不同,使用波片(waveplate)不能直接將它改變為平面偏振態光子。非偏振態光子可以描述為,處於 的機率是50%,處於 的機率是50%。它也可以描述為,處於垂直偏振態的機率是50%,處於水平偏振態的機率是50%。
非偏振態光子的量子態不是純態,而是由幾種純態依照統計機率組成。它可以由50%右旋圓偏振態與50%左旋圓偏振態組成,或者,它可以由50%垂直偏振態與50%水平偏振態組成。這兩種組合無法做實驗辨識區分,因此它們被視為同樣的混合態。密度算符含有混合態的所有資料,足夠計算任何關於混合態的可測量性質。
混合態到底源自何處?試想非偏振態光子是怎樣製成的。一種方法是利用處於動力學平衡的系統,這系統擁有很多個微觀態(microstate),伴隨每一個微觀態都有其發生的機率(波茲曼因子),它們會因熱力學漲落(thermal fluctuation)從一個微觀態變換到另一個微觀態。熱力學隨機性可以解釋白熾燈怎樣發射非偏振光子。另一種方法是引入不確定性於系統的製備程序,例如,將光束通過表面粗糙的雙折射晶體,使得光束的不同部分獲得不同偏振。第三種方法應用EPR機制,有些放射性衰變會發射兩個光子朝著反方向移動離開,這糾纏系統的量子態為 ,整個系統是處於純態,但是每一個光子子系統的物理行為如同非偏振態光子,從分析光子子系統的約化密度算符,可以得到這結論。
一般而言,混合態時常會出現於幾種純態的統計性混合(例如熱力學平衡)、製備程序的不確定性(例如光子可能移動於稍微不同路徑)、包含在糾纏系統內的子系統(例如EPR機制)。
純態
假設一個量子系統的量子態是純態,則這量子態可以用態向量表示為 ,對應的密度算符定義為[4]:309-313
- 。
從密度算符的形式,可以推論密度算符是自伴算符:
- 。
假設,物理量 是這量子系統的可觀察量,其本徵值為 的本徵態 形成一個規範正交基 ,則對可觀察量 做測量得到 的機率 為[5]:96-99
- ;
做實驗測量可觀察量 獲得的期望值為
- 。
這種可觀察量的期望值與跡數運算之間的關係稱為跡定則(trace rule)。[6]:36對於不同的規範正交基,跡數是個不變量。採用任何規範正交基,都可以計算出同樣跡數。[註 2]另外,機率公式與期望值公式對於密度算符都具有線性,這是很優良的性質,這意味著機率公式與期望值公式也適用於幾個密度算符的線性組合。
由於 被歸一化, 密度算符的跡數為1:
- 。
對於任意歸一化量子態 ,
- ,
所以,密度算符是非負算符(nonnegative operator)。
混合態
將先前純態密度算符的定義式加以延伸,假設在一個量子系統處於純態 、 、 、……的機率分別為 、 、 、……,則這混合態量子系統的密度算符 為[4]:311-313
- 。
每一個機率都是非負實值,所有機率的總和為1:
- ,
- 。
按照「無知詮釋」,這種量子系統確定是處於某個純態,但是無法知道到底是哪一個純態。這種可以用無知詮釋來論述的量子系統稱為「真混合物」(proper mixture),否則,稱為「瑕混合物」(improper mixture)。[7][註 3]
回想在純態段落裏,機率公式與期望值公式對於密度算符都具有線性,這意味著對於混合態的密度算符,這些公式也都適用。加以延伸後的密度算符,也具有先前純態的密度算符所擁有的性質:
- 密度算符是自伴算符: 。
- 密度算符的跡數為1: 。
- 對可觀察量 做測量得到 的機率為 。
- 做實驗測量可觀察量 獲得的期望值為 。
- 密度算符是非負算符: 。
由於密度算符 是自伴算符,它具有譜表示
- ;
其中, 是本徵值為 的本徵態,所有 形成一個規範正交基。
按照自伴算符的定義,每一個本徵值 是它自己的共軛:
- 。
由於密度算符 是非負算符,每一個本徵值 都是非負值。
由於密度算符 的跡數為1,
- 。
給定一個量子系統,其所有可能的密度算符組成一個凸集。假設 屬於這凸集,則 也屬於這凸集;其中, 是係數, 。[2]:51
用密度算符辨認純態與混合態
由於純態的密度算符定義式為[4]:311-313
- ,
所以純態的密度算符具有特徵
- 。
- 。
否則,非純態的密度算符遵守關係式
- 。
另外,將純態的密度矩陣 對角化後,只能有一個對角元素等於1,其它對角元素都等於0,例如,一種形式為[8]:178-183
- 。
量子態的純度 定義為
- 。
純態的純度為1。處於N維希爾伯特空間、完全混合的混合態,其對角元素的數值為 、非對角元素的數值為0,其純度為 。[6]:40-41
馮諾伊曼熵是另一種描述量子態混合程度的量度。
範例
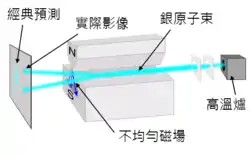
如右圖所示,使用z-軸方向的斯特恩-革拉赫實驗儀器,可以將入射的銀原子束,依照自旋的z-分量 分裂成兩道,一道的 為上旋,標記為 ,另一道的 為下旋,標記為 。
z-軸方向
- 態向量: 。
- 密度矩陣: 。
- 態向量: 。
- 密度矩陣: 。
x-軸方向
- 態向量: 。
- 密度矩陣: 。
- 態向量: 。
- 密度矩陣: 。
y-軸方向
- 態向量: 。
- 密度矩陣: 。
- 態向量: 。
- 密度矩陣: 。
完全隨機粒子束
完全隨機粒子束的量子態不是純態,它可以由50% 純態與50% 純態組成:
- 。
它也可以由50% 純態與50% 純態組成:
- 。
另外,它還可以由50% 純態與50% 純態組成,因此可見,不同的組合仍可得到同樣的混合態。
一般而言,完全隨機粒子束的 密度矩陣 ,經過對角化之後,可以寫為[8]:186
- 。
馮諾伊曼方程式
薛丁格方程式描述純態怎樣隨著時間流逝而演化,馮諾伊曼方程式描述密度算符怎樣隨著時間流逝而演化。實際而言,這兩種方程式等價,因為它們彼此都可以推導出對方。假設,在時間 ,量子系統的密度算符為
- ;
其中,量子系統在時間 處於純態 的機率是
假若不攪擾這量子系統,則機率 跟時間無關。在時間 ,純態 遵守含時薛丁格方程式
- ,
其中, 是約化普朗克常數, 是哈密頓算符。
- ;
其中,方括弧代表對易算符。
注意到只有當採用薛丁格繪景時(必須採用薛丁格繪景來計算密度算符)這方程式才成立,雖然這方程式看起來很像海森堡繪景的海森堡方程式,唯一差別是關鍵的正負號:
- ;
其中, 是某種採用海森堡繪景的算符。
在海森堡繪景裏,密度算符與時間無關,正負號差別確使期望值 對於時間的導數會得到與薛丁格繪景相同的結果。[註 4]
假若哈密頓算符不含時,則可從馮諾伊曼方程式推導出
- 。
馮諾伊曼熵

在量子統計力學(quantum statistical mechanics)裏,馮諾伊曼熵(von Neumann entropy)是經典統計力學關於熵概念的延伸。對於密度矩陣為 的混合態,馮諾伊曼熵定義為[12]:301
- 。
這公式涉及到矩陣對數(logarithm of a matrix),似乎很難計算,[註 5]但密度算符 是自伴算符,具有譜表示[8]:186-188
- ;
其中, 是本徵值為 的本徵態,所有 形成一個規範正交基。
因此,可以將密度矩陣 對角化,將馮諾伊曼熵更簡單地以對角化後的密度矩陣 定義為
- 。
馮諾伊曼熵 又可以寫為
- 。
從這形式,可以推論馮諾伊曼熵與經典信息論裏的夏農熵(Shannon entropy)相關。[12]
在這裏,可以視每一個本徵值 為處於本徵態 的機率。假若某事件的發生機率為零,則這事件不應貢獻出絲毫馮諾伊曼熵。從數學而言,以下極限為零:
- 。
因此,可以採用約定
- 。
純態的馮諾伊曼熵為零,因為其密度矩陣對角化之後,只有一個元素為1,其它均為0。即所有對角元素 必定滿足 或 。
完全隨機混合態的 密度矩陣,其馮諾伊曼熵 為
- 。
假若,將馮諾伊曼熵視為量子系統失序現象的一種量度,則純態擁有最小的馮諾伊曼熵 ,而完全隨機混合態擁有最大的馮諾伊曼熵 。
每一次做投影測量,馮諾伊曼熵都會增加,永遠不會減少,但是,對於廣義測量(generalized measurement),馮諾伊曼熵可能會減少。[13][14]混合態的馮諾伊曼熵永遠不小於零。因此,純態可以通過投影測量改變為混合態,但是,非純態的混合態永遠無法通過投影測量改變為純態。投影測量這動作促成了一種基本不可逆性的對於密度算符的改變,如同波函數塌縮。實際而言,相當反直覺地,投影測量這動作抹除了複合系統的量子相干性。更詳盡內容,請參閱條目量子退相干。
一個量子系統的子系統可以從混合態改變為純態,但是所附出的代價是其它部分的馮諾伊曼熵會增加,就好似將一個物體放進冰箱來降低其熵,冰箱熱交換器外的空氣會變暖,而所增加的熵會比物體所減少的熵更多。更詳盡內容,請參閱條目熱力學第二定律。
註釋
- 對於本徵態 的投影算符 ,假若作用於量子態 ,則會得到 與對應機率幅的乘積:
- ;
- 給定兩個規範正交基 ,對於任意算符 ,
- 。
- 在量子退相干裏,約化密度算符代表的是反常混合物,它不能被視為處於某個未知的純態;它是依賴環境與系統之間的相互作用使得所有的非對角元素趨於零,實際而言,這些非對角元素所表現的量子相干性已被遷移至環境,只有從整個密度算符才能查覺到這量子相干性的存在。[6]:48-49
- 在薛丁格繪景裏,純態隨著時間而演化的形式為
- 。
- 。
- 矩陣對數(logarithm of a matrix)也是矩陣;後者的矩陣指數等於前者。這是純對數的推廣。這運算是矩陣指數的反函數。並不是所有矩陣都有對數,有些矩陣有很多個對數。
參考资料
- von Neumann, John, , Göttinger Nachrichten, 1927, 1: 245–272
- Ballentine, Leslie. 2nd, illustrated, reprint. World Scientific. 1998. ISBN 9789810241056.
- Fano, Ugo, , Reviews of Modern Physics, 1957, 29: 74–93, Bibcode:1957RvMP...29...74F, doi:10.1103/RevModPhys.29.74.
- Laloe, Franck, , Cambridge University Press, 2012, ISBN 978-1-107-02501-1
- Griffiths, David J., , Prentice Hall, 2004, ISBN 0-13-111892-7
- Maximilian A. Schlosshauer. . Springer Science & Business Media. 1 January 2007. ISBN 978-3-540-35773-5.
- Bernard d' Espagnat. . Advanced Book Program, Perseus Books. 1999. ISBN 978-0-7382-0104-7.
- Sakurai, J. J.; Napolitano, Jim, 2nd, Addison-Wesley, 2010, ISBN 978-0805382914
- Dirac, P. A. M. . Mathematical Proceedings of the Cambridge Philosophical Society. 2008, 26 (3): 376. Bibcode:1930PCPS...26..376D. doi:10.1017/S0305004100016108.
- Breuer, Heinz; Petruccione, Francesco, : 110, ISBN 9780198520634
- Schwabl, Franz, : 16, 2002, ISBN 9783540431633
- Bengtsson, Ingemar; Zyczkowski, Karol. 1st.
- Nielsen, Michael; Chuang, Isaac, , Cambridge University Press, 2000, ISBN 978-0-521-63503-5. Chapter 11: Entropy and information, Theorem 11.9, "Projective measurements cannot decrease entropy"
- Everett, Hugh, , , Princeton Series in Physics, Princeton University Press: 128–129, 1973, ISBN 978-0-691-08131-1

