新月

新月、月缺，指月亮無光之月相，一種天文現象。月球在繞行地球的軌道上，介合於太陽和地球之間之時，就會呈現此月相；在此刻，月球背向太陽的黑暗面朝向地球，因此從地球上以肉眼看不見月球。夏曆以「朔」定義每月初一[1]。

  此條目介紹的是天文术语。关于文學刊物，请见「新月社」。关于五子棋开局名称，请见「新月 (五子棋)」。
描繪新月月相的圖片

名稱及含義
月相取決於月球在環繞地球軌道上的位置。這張是由北極上方鳥瞰的圖。

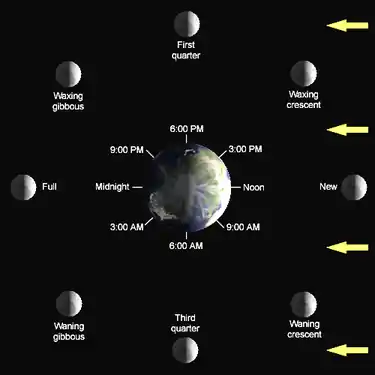
「新月」這個詞彙原本的意義是月球在與太陽合之後，最早被看見的眉月。這發生在太陽在西方地平線西沉，也就是日落之後一小段時間的月没之前，因此新月出現的日期和能看見此一事件的精確時間，與觀測者的地理位置有著密切的關聯性。天文學的新月（朔），有時也稱為「黑月」以免造成混淆，從定義看是發生在太陽和月球有著相同黃經的合，這時從地球上是看不見月球的。在此獨特時刻，月亮在太陽地球之間，且最接近一條直線，與觀測位置無關，而且在某些情況下它會發生日食。

新月原本的意義是最早被看見的眉月，因此在陰曆被做為一個月的開始，像是回曆和陰陽合曆的希伯來曆、印度曆和佛曆。但是在中國的農曆是以黑月（朔）做為一個月的開始。《說文》：「朔，月一日始蘇也。」古代中国历法中，朔日的計算方法有平朔和定朔两种。相對應的月末稱作晦，月圓稱作望，可能在每月的十五或十六日。而藏曆把每月十五日固定為望，朔則可能在月初或月末。伊斯兰历將新月初現定為每月第一天，朔則在月末前三四天。

现在“新月”为英語：的对意语，而在古籍中“新月”本来是“朔”之后第一次能看到的月球（因为“朔”的时候是看不见月亮的），时间大致为农历初二或初三，也称“三日月”，故有“一弯新月”的说法。弯钩月的图案也是众多美术品，以及伊斯兰教的常用图案。

近似推算公式

相鄰的兩個新月的間隔（陰曆月）是易變的，平均的間隔稱為朔望月，長度是29.53天。要計算新月（太陽與月球合）平均時刻的一個成功的慣用近似公式如下：

此處的N是一個整數，以2000年第一個新月為0開始計數，每經過一個朔望月數值就加1；結果的d是一個從2000年1月1日00:00:00起算的實數（帶有小數），而採用的時間是星曆表中的地球時（TT）。

通常以世界時（UT）表示這個時刻，要增加下式所得到的結果於d之上：

天

真實的合的時刻會因為週期性的攝動而從平均的時刻發生改變。從1601年至2401年的新月，最大的差異達到0.592天（14時13分）。陰曆月的時間（從一次朔至下一次朔）的變化在29.272天和29.833天之間，也就是比平均值短0.259天（6小時12分）至長0.302天（7小時15分）[2][3]。合的真實時刻和平均值之間的差異通常都比上述的範圍小，這是因為在一個陰曆月的週期中不可能所有的攝動值全部都達到它們的最大值的緣故。

參考滿月周期的文章，那兒有一個更簡單但更準確的計算朔的時刻的公式。

公式中長期項的誤差大約是：在地球時是1 cy²秒，在世界時是11 cy²秒（cy是2000年起的世紀數；參見「公式的解釋」有更詳細的說明。)

公式的解釋

合的平均時刻可以很容易的從月球平黃經減去太陽平黃經的算表中計算出來（迪羅尼參數D）。瓊·米斯在他的《天文學計算公式》一書中所給的計算公式是依據布朗和紐康的星曆表（ca. 1900），並且是他的《天文演算法》的第一版[4]，以ELP2000-85為基礎[5]（第二版在1998年，使用從Chapront et al.改進的ELP2000-82），這些現在都已經過時了（2002年）[6]。出版後改善了參數，並且米斯的公式使用可變的分數，可以做四種主要相位的計算，並且使用第二個變數做一般項目。為了讀者的方便，上述的公式根據Chapront最後修正的參數並且以單一的整數做為唯一的變數，並且加入了下列的項目：

常數項：
  • 如同米斯，使用的常數項是來自太陽的光行差和月球的光時改正[7]獲得在黃經度上的視黃經差：
太陽：+20.496"。[8]
月球：−0.704"。[9]
合的改正：−0.000451天。[10]
  • 對世界時：在2000年1月，ΔT (= TT − UT )是+63.83秒[11]；因此改正合的鐘錶時間UT = TT − ΔT 為：
−0.000739天。
二次項：
  • 在ELP2000–85（參見Chapront et alii 1988），D是一個二次項的函數，其值為 −5.8681"T²；陰曆月的數量用N表示，產生的修正式為+87.403×10–12N²[12]，得到與合的時刻相差的天數。這個項目內包含了0.5×(−23.8946 "/cy²)的潮汐加速。目前最佳的估計是來自月球雷射陣列的加速度（參見Chapront et alii 2002）：(−25.858 ±0.003)"/cy²。因此，新的二次項參數D是 -6.8498"T²[13]。實際上，Chapront et alii（2002）提供了多項式的証明，在他們的表4也提供了相同的証明。這項轉換修改了到合的時刻為+14.622×10−12N²天；這個二項式現在成為：
+102.026×10−12N²天。
  • 對世界時（UT）：對歷史上的觀測分析顯示ΔT有著+31 s/cy²的長期增量[14]。轉換成天和陰曆月[15]，從ET轉換成UT的修正是：
−235×10−12N²天。

理論上潮汐對ΔT的貢獻大約是+42 s/cy²[16]，更小的觀測值被認為主要歸因於地球形狀的變化[17]，由於誤差不能被充分的解釋（地球轉動的角度），我們對UT預測的不確定性可能大到11 s/cy²；在與太陽合時，月球位置的誤差上可能只有0.5"/cy²[18]，或是（因為月球的平均視角速度大約是0.5"/s）1 s/cy²。

宗教上的應用
参见：陰曆
  • 回曆保留了新月在觀測上的定義，以實際看見新月的時刻做為一個月的開始，因而使它不可能在朔之前就開始一個新的月份（特別是，齋戒月開始的確切日期無法事先就知道）。在沙烏地阿拉伯，當期望中的新月該出現時若遇上陰天，觀測人員會被送上飛機到雲層之上觀測。在巴基斯坦，有一個"中央 Ruet-e-Hilal委員會"，由國家協助巴基斯坦氣象局超過100個的觀測所，在全國各地確認是否看見新月，並且統一宣布每一個月的開始。在伊朗，由一個特別的委員會審視來自各地的新月報告，這個委員會有100個觀測委員小組，以確定每個月的開始。

相關條目

參考資料
  1. . 香港中文大學.
  2. Jawad, Ala'a H. Roger W. Sinnott , 编. . Sky&Telescope. Nov 1993: pp.76..77.
  3. Meeus, Jean. . Willmann-Bell, Richmond VA USA. 2002: 19..31. ISBN 0-943396-74-3.
  4. formula 47.1 in Jean Meeus (1991): Astronomical Algorithms (1st ed.) ISBN 978-0-943396-35-4
  5. M.Chapront-Touzé, J. Chapront (1988): "ELP2000-85: a semianalytical lunar ephemeris adequate for historical times". Astronomy & Astrophysics 190, 342..352
  6. J.Chapront, M.Chapront-Touzé, G. Francou (2002): "A new determination of lunar orbital parameters, precession constant, and tidal acceleration from LLR measurements 页面存档备份，存于". Astronomy & Astrophysics 387, 700–709
  7. Annual aberration is the ratio of Earth's orbital velocity (around 30 km/s) to the speed of light (about 300,000 km/s), which shifts the Sun's apparent position relative to the celestial sphere toward the west by about 1/10,000 radian. Light-time correction for the Moon is the distance it moves during the time it takes its light to reach Earth divided by the Earth-Moon distance, yielding an angle in radians by which its apparent position lags behind its computed geometric position. Light-time correction for the Sun is negligible because it is almost motionless during 8.3 minutes relative to the barycenter (center-of-mass) of the solar system. The aberration of light for the Moon is also negligible (the center of the Earth moves too slowly around the Earth-Moon barycenter (0.002 km/s); and the so-called diurnal aberration, caused by the motion of an observer on the surface of the rotating Earth (0.5 km/s at the equator) can be neglected. Although aberration and light-time are often combined as planetary aberration, Meeus separated them (op.cit. p.210).
  8. Derived Constant #14 from the IAU (1976) System of Astronomical Constants (proceedings of IAU Sixteenth General Assembly (1976): Transactions of the IAU XVIB p.58 (1977)); or any astronomical almanac; or e.g. 页面存档备份，存于
  9. formula in: G.M.Clemence, J.G.Porter, D.H.Sadler (1952): "Aberration in the lunar ephemeris", Astronomical Journal 57(5) (#1198) pp.46..47 ; but computed with the conventional value of 384400 km for the mean distance which gives a different rounding in the last digit.
  10. Apparent mean solar longitude is −20.496" from mean geometric longitude; apparent mean lunar longitude −0.704" from mean geometric longitude; correction to D = Moon − Sun is −0.704" + 20.496" = +19.792" that the apparent Moon is ahead of the apparent Sun; divided by 360×3600"/circle is 1.527×10−5 part of a circle; multiplied by 29.53... days for the Moon to travel a full circle with respect to the Sun is 0.000451 days that the apparent Moon reaches the apparent Sun ahead of time.
  11. see e.g. . [2006-12-17]. （原始内容存档于2007-02-02）.; the IERS is the official source for these numbers; they provide TAI−UTC here and UT1−UTC here; ΔT = 32.184s + (TAI−UTC) − (UT1−UTC)
  12. delay is − (−5.8681") / (60×60×360 "/circle) / (36525/29.530... lunations per Julian century)² × (29.530... days/lunation) days
  13. −5.8681" + 0.5×(−25.858 − −23.8946)
  14. F.R. Stephenson, Historical Eclipses and Earth's Rotation. Cambridge University Press 1997. ISBN 978-0-521-46194-8 . p.507, eq.14.3
  15. 31 s / (86400 s/d) / [(36525 d/cy) / (29.530... d/lunation)]²
  16. Stephenson 1997 op.cit. p.38 eq.2.8
  17. Stephenson 1997 op.cit. par.14.8
  18. from differences of various earlier determinations of the tidal acceleration, see e.g. Stephenson 1997 op.cit. par.2.2.3

外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.