標記 (幾何)

在多面體幾何學中，標記（flag）[1]是指多胞形中的一系列維面，並且在這個序列中各包含了每個維度的其中一個元素。例如正方形中，正方形（ABCD）與其中一條稜（AB）與稜上一點（A）與其子集空多胞形（Ø）這四個正方形中的元素構成了一個正方形的標記，而正方形（ABCD）與其中一條稜（CD）與該正方形的另一條稜（AB）與稜上一點（A）與其子集空多胞形（Ø）這五個正方形中的元素構成的序列則不算是正方形的標記。

立方體的其中一個標記，其包括了立方體本身、其中一個正方形面、該面的其中一條稜、稜上的一個頂點以及這個立方體中「什麼都不選」的子集，即空多胞形，五個元素，正好每個維度各一個元素，且較大的元素包含較小的元素。
四角錐的維面圖，塗上紅色的部分為四角錐的其中一個標記。

定義

較正式的多胞形標記的定義為，n維多胞形的標記ψ是一個集合{F−1, F0, ..., Fn}，使得Fi ≤ Fi+1，其中−1 ≤ i ≤ n − 1，並且對於每個i，ψ中恰好存在一個的Fi，其中i滿足−1 ≤ i ≤ n。[2][3]但是，由於維度最小的元素F−1和維度最大的元素Fn必須在每個標記中，因此在表達一個標記時通常會被省略，並且有時會被稱為不標準的多面體元素。[4]

舉例來說，一個多面體的標記會包含一個頂點、一條含前述頂點的稜、一個含前述稜的面以及一個空多胞形和多面體本身。[5]

如果一個幾何圖形或結構的對稱性可以在其標記上傳遞的，則這個個幾何圖形或結構可以被認為是正圖形。[6] 但這個定義並不包括手性圖形[7]。

標記多胞形

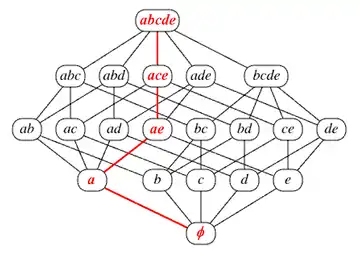
若一個多胞形，其所有元素的子集都是該多胞形的標記，則稱該多胞形為標記多胞形（）[8]。其可以對應到複形中的團複形的概念，其也與圖論中的團概念相關。在圖論中，團是滿足兩兩之間有邊連接的頂點的集合[9]，而團複形本身就是一個團，且該集合中的每個子集也位於團複形中，[10]因此團複形有時稱為標記複形（） [11]。另外一種定義是若一多胞形中，任何一組互相相交的一系列維面中，若每個維面元素的集合之交集並非空集，則該多胞形稱為標記多胞形[12]，這個定義與前述不同，但實際上等價[13]。例如立方體是一個標記多胞形但截角四面體不是[14]。

若一個多胞形是標記多胞形，則其維面也同樣會是標記多胞形。[15]

重合幾何

在探討具有在其元素上定義重合關係（具有對稱和反射關係）的集合，即更抽象的重合幾何環境中，標記是一組互相具有重合關係的元素。[16]:3這種抽象概念概括了多面體幾何學中的標記概念以及線性代數中的標記概念。[17]

秩為r的重合幾何物件（Ω, I）可以被分割成集合Ω1, Ω2, ..., Ωr，使得每個集合的每個最大的標記恰好在一個元素中，其中最大的標記代表著不包含在任何標記中的標記。在此例中，Ωj的元素稱為j類元素。因此，在秩為r的重合幾何物件中，每個最大標記都恰好具有r個元素。[18]

秩為2的重合幾何物件通常稱為重合結構，在重合結構中，類型為1類的元素稱為點，類型為2類的元素稱為區塊（某些情況稱為線）[16]:5

重合結構是一個三元組D = (V, B, I)，其中V和B是任意兩兩不交的集合，I是V和B之間的二元關係，即I ⊆ V × B。其中V的元素稱為點、B的元素稱為區塊、I的元素稱為標記。[19]

用途

在正多胞形中，標記可以用於簡化正多胞形的定義。一般正多胞形的定義是要同時滿足每個維度上的每個元素在其對稱性上可以傳遞，該圖形才屬於正圖形，例如正多面體[20][21]，其中特性可傳遞，簡稱可遞，意味著若該幾何結構中任意兩個同類元素元素A和B，透過在該幾何結構的對稱性下的變換（如旋轉或鏡射這個幾何結構），使A移動到B原來的位置時，其元素仍然佔據了相同的空間區域[22]。然而標記是指個包含所有維度中元素，每個維度的元素個一個的集合，因此透過討論標記可遞與否就能判斷該立體是否為正圖形[6]，然而此定義無法確認手性圖形是否為正圖形[7]。

參見

參考文獻
  1. . 雙語詞彙資料庫, 國家教育研究院.
  2. Hartley, Michael I. . Periodica Mathematica Hungarica (Springer). 2006, 53 (1-2): 149––156.
  3. (PDF). fields.utoronto.ca.
  4. D’Azevedo, Antonio Breda and Jones, Gareth A and Schulte, Egon. . Canadian Journal of Mathematics (Cambridge University Press). 2011, 63 (6): 1254––1283.
  5. Blatov, VA and O'keeffe, M and Proserpio, DM. . CrystEngComm (Royal Society of Chemistry). 2010, 12 (1): 44––48.
  6. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8.
  7. Schulte, Egon. . Discrete & Computational Geometry (Springer). 2005, 34 (2): 181––229.
  8. Adiprasito, Karim Alexander. . arXiv preprint arXiv:1403.2657. 2014.
  9. Luce, R. Duncan; Perry, Albert D., , Psychometrika, 1949, 14 (2): 95–116, PMID 18152948, doi:10.1007/BF02289146
  10. Bandelt, H.-J.; Chepoi, V., , Goodman, J. E.; Pach, J.; Pollack, R. (编), (PDF), Contemporary Mathematics 453, Providence, RI: AMS: 49–86, 2008
  11. Frohmader, Andrew. . Israel Journal of Mathematics (Springer). 2008, 164 (1): 153––164.
  12. Alastair, D. and Jelena, G. and Zhi, L. . Lecture Notes Series, Institute For Mathematical Sciences, National University Of Singapore. World Scientific Publishing Company. 2017: 83. ISBN 9789813226586.
  13. Buchstaber, V.M. and Pano, T.E. . Mathematical Surveys and Monographs. American Mathematical Society. 2015. ISBN 9781470422141. LCCN 15006771.
  14. Victor Buchstaber, Nikolay Erokhovets. (PDF). 大阪市立大学 大学院理学研究科・理学部. June, 2015.
  15. Erokhovets, Nikolai. . arXiv preprint arXiv:1501.03801. 2015.
  16. Beutelspacher, Albrecht; Rosenbaum, Ute, , Cambridge: Cambridge University Press, 1998, ISBN 0-521-48277-1
  17. Shafarevich, I. R.; A. O. Remizov. . Springer. 2012. ISBN 978-3-642-30993-9.
  18. De Bruyn, Bart. . Birkhäuser. 2016.
  19. Beth, Thomas; Jungnickel, Dieter; Lenz, Hanfried. . Cambridge University Press. 1986: 15.. 2nd ed. (1999) ISBN 978-0-521-44432-3
  20. Gardner (1987): Martin Gardner wrote a popular account of the five solids in his December 1958 Mathematical Games column in Scientific American.
  21. Zeyl, Donald. . .
  22. McLean, K. Robin, , The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.