雙角錐柱
在幾何學中,雙角錐柱又稱為雙棱锥柱、長雙錐體(英語:),是指一系列的多面體,一個柱體上下二個底面都階上一個底面全等的錐體,或是一個雙錐體,拆開來後插入一個柱體所構成的幾何體。若雙角錐柱的底面為正多邊形則稱為正角錐柱,每個面皆為正多邊形的正雙角錐柱只有三種:正雙三角錐柱、正雙四角錐柱及正雙五角錐柱,同時,它們也是詹森多面體。
| 雙角錐柱 | |
|---|---|
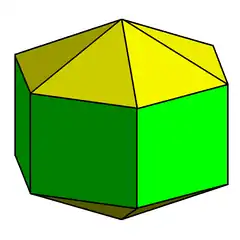 以雙六角錐柱為例 | |
| 類別 | 雙角錐柱 |
| 面 | 3n |
| 邊 | 5n |
| 頂點 | 2n+2 |
| 歐拉特徵數 | F=3n, E=5n, V=2n+2 (χ=2) |
| 面的種類 | 2n個三角形 n個矩形 |
| 對稱群 | Dnh, [n,2], (*n22) |
| 對偶 | 雙錐台 |
| 旋轉對稱群 | Dn, [n,2]+, (n22) |
| 特性 | 凸、 demi-regular |
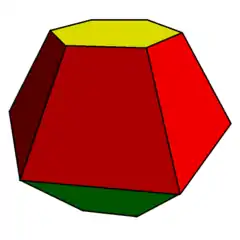 雙錐台 (對偶多面體) | |
雙角錐柱與角錐柱十分類似,雙角錐柱可以看做是角錐柱弟底面與一個底面全等的錐體相接;而角錐柱也可以看做是雙角錐柱切除一個錐體,就如同偏方面體與半偏方面體之關係。
詹森多面體
如同正角錐柱,在不退化的情形下,所有正角錐柱中包含了三種詹森多面體,即:雙三角錐柱、雙四角錐柱及雙五角錐柱。
| 名稱 | 面 | dual | |
|---|---|---|---|
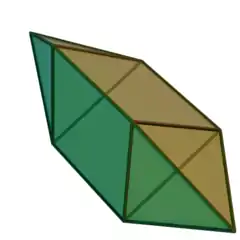 | 雙三角錐柱 (J14) | 6個三角形、3個正方形 | 雙三角錐台 |
 | 雙四角錐柱 (J15) | 8個triangles、4個正方形 | 雙四角錐台 |
 | 雙五角錐柱 (J16) | 10個triangles、5個squares | 雙五角錐台 |
 | 雙六角錐柱 | 12個triangles、6個squares | 雙六角錐台 |
| 雙n角錐柱 | 2n triangles、n squares | 雙錐台 |
參考文獻
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller. . Consultants Bureau. 1969. No ISBN. The first proof that there are only 92 Johnson solids.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
