震源
震源(英語:[註 1]),宏观上是指地震能量大量释放之处,而微观上是指首先发生地震波的地方,通常指地下岩层断裂错动的地区[2]。在测震领域中,常将震源看作是一个理想化的面源或点源[3]。其对应的震源深度——即震源垂直向上到地表的距离——也是最重要的地震基本参数之一。震级相同的地震,震源越深,影响范围越大,地表破坏越小;震源越浅,影响范围越小,地表破坏越大[4]。一般地,使用米(m)或千米(km)作为震源深度的单位,用拉丁字母h作为符号表示震源深度。浅源地震的深度误差约为深度值的10%左右。震源愈深,相对误差愈小[5]。
| 系列条目 |
| 地震 |
|---|
| 孕震与监测 |
|
|
| 防震与减灾 |
| 地震学研究 |
|
地震专题 地球科学主题 • 本年地震 |
研究历史
1910年,美国地震学家里德发表弹性回跳理论,作出地震发震原因的假设,给出了地震和地球物质破坏的假说,提出了断层破裂和震源的概念[6]。美国学者特纳则于1922年证明了某些地震的震源深度可以大于通常地震的震源深度,提出了深源地震的概念[7]。1930年代节线的发展进一步推动了对震源的研究[8]。日本地震学家和达清夫利用十几年时间对日本海海域的深源地震展开了调查,于1935年完成深源地震图像的制作,对日本海深源地震分布进行了归纳总结,证明了深源地震的存在[9][10]。随后,和达清夫和胡戈·班尼奧夫各自通过独立研究发现了和达-贝尼奥夫带,获知了触发深层地震的原因[11][12]。1938年,美国学者拜尔利发展了震源机制求解法,首次用P波初动求出了完整的地震断层面解[6]。
其后,对震源的研究进入了为期三十余年的瓶颈期[13]。发展缓慢的原因大致可归结为两方面:一是地球内部结构研究对国民经济和社会发展关系重大,自然资源的勘探和地下核爆炸的侦查困难较多;二是震源研究难度较大,它的研究主要依赖于反映地震的动力学特性的地震波波形,地震波波形受到震源过程、传播介质以及仪器等各方面的影响[14][15]。
1950年,可控震源在美国首次出现,并于1957年投入实际应用[16]。1954年,苏联方面启动了对地下核爆炸引起地壳构造变动过程的研究[17]。1957年9月19日,美国在内华达试验场进行了第一次地下核试验[18]。同年9月,在多伦多国际大地测量学与地球物理学联合会(IUGG)的大会上,地球物理学家布伦(K. E. Bullen)作了题为《我们原子时代的地震学》的报告,公开发布了对该次核试验核爆地震震源的研究结果,引起了地球物理学界和社会公众的极大反响[18][19]。
20世纪60年代之后,震源研究进入快速发展期[13]。1961年以后,可控震源作为通用地震勘探工具开始在石油勘探等领域广泛使用[16]。苏联联合地震观测台网亦从当年起率先投入地下核试验监测工作[20]。1960年代中期,许多研究机构扩充了地震学方向的物质破裂物理学室内实验队伍 ,并将研究方向放在了对剪切破坏条件下微裂隙和宏观裂隙的形成过程及伴随此过程的样品与模型物理—力学性质的变化过程研究上[8]。同时,野外预报研究也取得了进展,并确认了地球各不同地区中发现的部分前兆具有与地震能量有关的类似的时间过程[8]。1960年代末,日本学者笠原庆一提出了发震孕育时间的概念[21]。1970年代,中国地球物理学家傅承义提出了“红肿”假说,他认为地震发生前有一个形如“红肿区”的孕育区[13]。同一时期,中国科学院也在其地球物理研究所下设置了震源物理研究室,这是中国大陆首个震源物理研究的专门机构[13]。苏联研究人员其后提出了孕震期间和未来震源周围区域的概念,发展和完善了震源物理学科[13]。苏联亦于1970年代末成立了苏联科学院地球物理研究所震源物理研究集体,作为震源物理研讨研究的学术专门团体[13]。
21世纪初,美国开始在加利福尼亚州等州和地中海地区、日本等地布设了稀疏宽带台网,这是一般数字台阵在震源物理方面的较早应用[22]。德格雷德和帕西亚诺姆利用该台网的记录,采用时间域反演方法,推导取得了地震序列的地震矩张量数据,对此前震源物理张量解的研究方法进行了平行实验,并了解了震源过程子破裂的部分细节[22][23]。
测定方法
测定震源,首先需要测定震中。在20世纪以前,测定震中的方式一般为几何中心法。随着地震学的发展,在地震仪等仪器技术逐步趋向于成熟后,便诞生了方位角法(单台测定法)和台网测定法。测定震中位置后,再测定震源深度h即可测出震源位置。使用石川法、和达法和走时表法等可以测定和计算震源深度[24]。
震中测定方法
测定近震震源位置和远震震源位置的方法不尽相同,且各有很多方法。但是基本可分为两类:一类是根据方位角测定震中[註 2],另一类是根据走时测定震中。在实际观测中,地震区单台记录到某些微弱的地方性地震和一些近震,但其他地区的地震台往往没有记录地不够精确甚至没有记录到。因此,必须谋求单台测定震源位置的方法,以便及时掌握当地地震活动的动态。同时,一个较大规模的地震发生后,虽然根据本台的记录可以判断该地震的远近,但却不知道具体发生的地方,一般需要靠台网多台测定后,才能知道震中位置[24]。
几何中心法
20世纪以前,在没有仪器记录时,地震的震中位置都是按破坏范围而确定的宏观震中,它是极震区(震中附近破坏最严重的地区)的几何中心。由于无法确定极震区的精确范围,通常会造成误差[25]。
方位角法(单台测定法)
由于各种地震波在不同地区、不同深度传播的速度都不同,波速快的或走直径的[註 3]先到达测站,其后陆续有其他波到达,这就产生了时间差。将震中距、震源深度和记录到的各种波的时间差,就可以编成适合各地使用的时距曲线及走时表。在某地发生地震时,分析员从地震记录图上量出该地震事件的各种波[註 4]的时间差,对照已编好的走时表或套用公式计算,便可得出震中距。随后便需要确定方位角。将两个水平方向的初动振幅化为地动位移,用三角函数便可求出方位角。当方位角和震中距都求出来后,便能够容易地找到震中位置。这种方法便称之为单台测定法[26]。
台网测定法
当至少三个地震测站计算出震中距时,便可通过三边量測法确定震中的位置[27]。这种通过仪器测量出的震中一般称之为微观震中的方法被称为台网测定法[24][註 5]。具体做法是,分别以三个台站为圆心,以各自求得的震中距按相应比例作半径在地图上画圆。然后,将每两个圆的交点连接,三条弦的交点即为所求得的震中,再换算出经纬度[26]。交切法初定的震中精度往往不高。其误差最好的情况为±0.3°,一般可达1°,所以必须要对其进行进一步修订[24]。
石川法
以地震台为圆心O、震源距离D为半径R构成一个球面,此球面在地面的截线就是同样的一个圆。三个圆相交可作出三条弦,三条弦的交点就是震中。过震中和任一地震台引线,作通过震中于台引线的垂线弦,则弦长的一半即为震源深度h[24]。然而,这种方法被认为误差较大[28]。
和达法
和达球面方程相应的球面称为和达球面。球心在地面上,球面与地面相交的圆,称为和达圆。各个地震台组合的和达圆的公共弦交点就是震中。过震中而垂直于过震中的半径的弦的二分之一为震源深度h[24]。然而,这种方法被认为误差较大[28]。
有限断层震源模型
由于地震滑动中心的位置,既受到断层整体大小的影响,又受到断层滑动(或应力)小尺度变化的影响,对地面运动产生了很大影响。因此,大地震的地面运动强烈地依赖于一个更趋向于局部性的方向性效应,即震源的位置可能会受到高滑动区域的影响[29]。有限断层震源模型是由日本学者小次郎入仓于2000年所提出的一种测定震源的模型。这种模型参数分为2类,分别为用来表征震源区宏观特征的全局震源参数和用来表示断层面上的不均匀性或粗糙度的局部震源参数。该模型首先根据地震构造背景和活动性调查等资料,确定出活断层的空间方位和滑动类型。其次,根据地震危险性评价判定的矩震级,根据经验关系是确定各种参数的值。在断层破裂面上划分1 km×1 km的网格,对每个网格赋予相对的滑动值。再将断层破裂面离散为2M×2N个网格,然后进行插值和平滑。最后,用傅氏变换将上述模型从空间域变化至波数域[30]。
相关研究
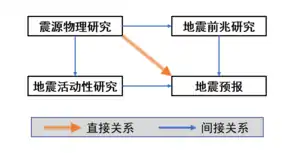
测定震源参数并提高其测量的精确度,是近代地震学研究的基本问题之一。因此,测定地震的基本参数一直是测震工作者日常从事并奋力精确化的课题。随着应用数学和电子计算机的发展并应用于地震学领域,以及地震学本身观测系统的改观,使得精确测定地震基本参数的工作有了重大进展[24]。
地震分类
- 按照震源深度的不同,通常可把地震分为三类:
- 浅源地震:震源深度小于60千米的地震。
- 中源地震:震源深度在60千米到300千米范围内的地震。
- 深源地震:震源深度大于300千米的地震。
震相研究
由于受到震源、震源深度、震中距及地震射线的传播综合影响,反映在地震记录图上震相表现的形态亦不相同。因此,随着震中距的不同,地震参数的测定也就不同。已知观测点的震中距,就可以较为轻松地分辨复杂而各异的震相,一般根据记录图上地震记录的总情况加以判断。地震的大小、远近、深远各有明显的特征。震源越近,震动的持续时间越短;震源越远,则持续时间越长[35]。
在震相研究中,震源机制解是用地球物理学方法判别断层类型和地震发震机制的一种方法。一次地震发生后,通过对不同的地震台站所接受到的地震波信号进行数学分析,即可求出其震源机制解。震源机制解不仅可以使人了解断层的类型(是正断层、逆断层还是走滑断层),而且可以揭示断层在地震前后具体的运动情况[36][37]。
注释
参考文献
- . United States Geological Survey. [2017-10-27]. (原始内容存档于2010-03-15) (英语).
- 中华人民共和国地质矿产部地质辞典办公室. . 地质出版社. : 200 (中文(简体)).
- 张路; 王威. . 地震. 1994, 2: 20–27 [2018-08-15] (中文(简体)).
- . 福建省数字地震科普馆. 2011-07-16 [2017-10-27]. (原始内容存档于2017-10-27) (中文(简体)).
- C Thurber. . Physics Today. 2003, 10: 66–67 [2017-10-27] (英语).
- 王鹏伟. . 中国地震学会历史地震、地震预报专业委员会2013年学术研讨会. 2013 [2018-08-15] (中文(简体)).
- . 中国地震台网. [2018-08-16]. (原始内容存档于2018-01-18) (中文(简体)).
- M•A•萨多夫斯基; 许同春. . 北京: 地震出版社. 1982-05 (中文(中国大陆)).
- 干微; 金振民; 吴耀; 赵素涛. . 地学前缘. 2012, 19 (4): 15–29 [2018-08-16] (中文(简体)).
- 孙文斌. . 防灾减灾学报. 1986, 1: 82–84 [2018-08-16]. doi:10.13693/j.cnki.cn21-1573.1986.01.010 (中文(简体)).
- Related Articles. . Britannica.com. [2018-08-16]. (原始内容存档于2012-09-04) (英语).
- . 美国地质勘探局. [2018-08-16]. (原始内容存档于2012-09-04) (英语).
- 耿乃光. . 国际地震动态. 1984, 8: 3–4+33–34 [2018-08-15] (中文(简体)).
- 刘万琴; 郑治真. . 《地震研究》. 1989, 1: 63–67 [2017-10-27] (中文(简体)).
- . 知网. [2018-08-15] (中文(简体)).
- 冯德益. . 国际地震动态. 1979, (5): 2–3 (中文(中国大陆)).
- 卜晓红. . 国际地震动态. 2002, (5): 88–91 (中文(中国大陆)).
- 吴忠良. . 物理. 2007, 36 (7) (中文(中国大陆)).
- 刘代志; 吴晓露; 李夕海. . 国家安全地球物理学术研讨会. 2007 (中文(中国大陆)).
- Adus; 黄志斌. . 防灾博览. 1996, (3): 3–4 (中文(中国大陆)).
- . 知网. [2018-08-15] (中文(简体)).
- 朱元清; 宋治平; 赵志光. . 国际地震动态 8. 2005: 1–7 [2018-08-15]. doi:10.3969/j.issn.0253-4975.2005.08.001 (中文(简体)).
- Dreger D.; Uhrhammer R.; Pasyanos M. . Bulletin of the Seismological Society of America. 1998, 88 (6): 1353–1362 [2018-08-15] (英语).
- 阎志德. . 山西地震. 1981, 4: 3–38 [2017-10-27] (中文(简体)).
- 马在田. . 石油地球物理勘探. 1979, 1: 48–50 [2017-10-19]. doi:10.13810/j.cnki.issn.1000-7210.1979.01.007 (中文(简体)).
- 石鹏. . 深圳特区科技. 1990, 4: 39 [2017-10-27] (中文(简体)).
- . Pennstate Earthquake Seismology. [2017-10-27]. (原始内容存档于2017-06-11) (英语).
- 马秀芳. . 地震研究. 1982, 1: 101–115 [2018-08-15] (中文(简体)).
- Mai P. M.; Spudich P.; Boatwright J. . Bulletin of the Seismological Society of America. 2005, 95 (3): 965–980 [2018-08-15]. doi:10.1785/0120040111 (英语).
- 王海云; 谢礼立; 陶夏新. . 地球科学 (中国地质大学). 2008, 33 (6): 843–851 [2018-08-15]. doi:10.3321/j.issn:1000-2383.2008.06.013 (中文(简体)).
- . 安徽省防震减灾信息网. 2010-09-27 [2017-10-27]. (原始内容存档于2017年10月27日) (中文(简体)).
- . 网易科技. 2004-10-27 [2018-08-15]. (原始内容存档于2018-08-15) (中文(简体)).
- 薛艳. . 中国地震局地球物理研究所. 2012 [2018-08-23]. (原始内容存档于2016-04-22) (中文(简体)).
- . 天气网. 2014-04-02 [2017-10-27]. (原始内容存档于2017-10-27) (中文(简体)).
- 邹立晔. . 国际地震动态. 2004, 10: 1–8 [2017-10-27]. doi:10.3969/j.issn.0253-4975.2004.10.001 (中文(简体)).
- Sipkin, S.A., 1994, Rapid determination of global moment-tensor solutions: Geophysical Research Letters, v. 21, p. 1667–1670.
- Sibuet,J-C.; Rangin,C.; Le Pichon,X.; Singh,S.; Graindorge,D.; Klingelhoefer,F.; Lin,J-Y.; Malod,J.; Maury,T.; Schneider,J-L.; Sultan,N.; Umber,M.; Yamuguchi,H.; the "Sumatra aftershocks" team. (PDF). Earth and Planetary Science Letters. 2004-12-16, 263: 88–103 [2018-08-15]. (原始内容 (PDF)存档于2008-05-27) (英语).

