三面體
在幾何學中,三面體(英文:Trihedron)是指由3個面組成的多面體。面為平面的三面體在三維空間不能存在,因為要至少四個頂點才能在三維空間形成有體積的多面體,除非它的面是曲面,或是存在四維超球面。此外,有一種抽象射影多面體是三面體,即立方體半形[1]。
| 部分的三面體 | |
|---|---|
 三面形 |
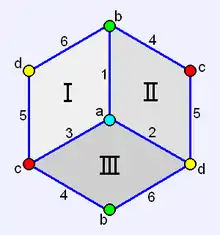 半立方體 |
常見的三面體
由於三維空間中的單純形是四面體,面數少於4的多面體都只能成為退化多面體[2],因此三面體都不能真正具有體積。在球面鑲嵌中,常見的三面體是三面形。亦有一種正抽象多面體是三面體,其為半立方體。
| 名稱 | 種類 | 圖像 | 符號 | 頂點 | 邊 | 面 | χ | 面的種類 | 對稱性 |
|---|---|---|---|---|---|---|---|---|---|
| 三面形 | 多面形 退化多面體 |
 |
{2,3} |
2 | 3 | 3 | 2 | 3個二角形 |
D3h, [2,3], (*223), order |
| 皮特里正四面體 | 皮特里對偶 | 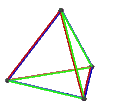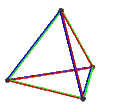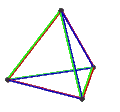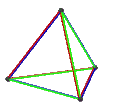 |
{3,3}π | 4 | 6 | 3 | 1 | 3個正扭歪四邊形 |
|
| 立方體半形 | 射影多面體 抽象多胞形 |
 |
{4,3}/2 {4,3}3[3] |
4 | 6 | 3 | 1 | 3個正方形 |
S4, order 24 |
| {6,3}1,1 | 環形多面體 | 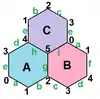 |
{6,3}1,1 | 6 | 9 | 3 | 0 | 3個正六邊形 |
|
| 圓柱體 | 非嚴格多面體 曲面 柱體 |
 |
0 | 2 | 3 | 1 | 1個曲面 2個圓形 |
三面形
| 三面形 | |
|---|---|
 (點選觀看旋轉模型) | |
| 類別 | 多面形、均勻多面體、球面鑲嵌 |
| 面 | 3 |
| 邊 | 3 |
| 頂點 | 2 |
| 歐拉特徵數 | F=3, E=3, V=2 (χ=2) |
| 面的種類 | 二角形 |
| 考克斯特符號 | |
| 施萊夫利符號 | {2,3} |
| 威佐夫符號 | 2 2 |
| 對稱群 | D3h, [2,3], (*223), order 12 |
| 對偶 | 三角形二面體 |
| 旋轉對稱群 | D3, [2,3]+, (223), order 12 |
儘管面為平面的三面體在三維空間不能存在,但在球面幾何學中,三面體可以以球面鑲嵌的方式存在,最簡單的例子是三面形。一個正三面形,表示三個鑲嵌在球體上的球弓形,施萊夫利符號中利用{2,3}來表示,其對偶多面體是三角形二面體。
性質
三面形是一個退化的多面體,其無法擁有體積。三面形由3個二角形組成,每個頂點都是3個二角形的公共頂點。正三面形的每個面都是正二角形,且每個頂點都是3個正二角形的公共頂點,因此正三面形也可以視為一種正多面體,但是因為其已退化,因此不會與柏拉圖立體一同討論。
三面形具有 D3h, [2,3], (*223) 的對稱性和 D3, [2,3]+ 的旋轉對稱性,且階數為12,在考克斯特符號中用![]()
![]()
![]()
![]()
![]() 表示。
表示。
圓柱
圓柱也能算是一種非嚴格的三面體,因為它可以看做是只有三個面的幾何體,由一曲面(側面)和兩個圓形平面(底面)所組成。
相關形狀
三胞體
三胞體是指有三個胞或維面的多胞體。其為三面體在四維或更高維度的類比,但由於四維空間的單純形是五胞體,任何面數邊樹或頂點數小於單純形的圖形都只能退化或成為球面鑲嵌,即無法具有非零的體積。
參見
參考文獻
- McMullen, Peter; Schulte, Egon, , 1st, Cambridge University Press: 162–165, December 2002, ISBN 0-521-81496-0
- Sloane, N.J.A. (编). . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- N. Wedd. . weddslist.com. 2010 [2016-08-14]. (原始内容存档于2019-05-02).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
