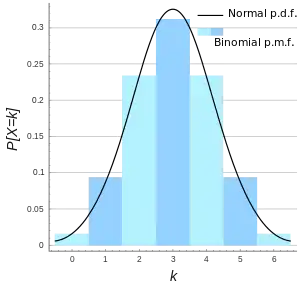
二項式分布

一般地，如果随机变量${\displaystyle {\mathit {X}}}$服从参数为${\displaystyle {\mathit {n}}}$和${\displaystyle {\mathit {p}}}$的二项分布，我们记${\displaystyle X\sim b(n,p)}$或${\displaystyle X\sim B(n,p)}$。n次试验中正好得到k次成功的概率由概率质量函数给出：

${\displaystyle f(k,n,p)=\Pr(X=k)={n \choose k}p^{k}(1-p)^{n-k}}$

对于k = 0, 1, 2, ..., n，其中${\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}}}$

是二项式系数（这就是二项分布的名称的由来），又记为C(n, k)，_nC_k，或ⁿC_k。该公式可以用以下方法理解：我们希望有k次成功(p^k)和n − k次失败(1 − p)^{n − k}。然而，k次成功可以在n次试验的任何地方出现，而把k次成功分布在n次试验中共有C(n, k)个不同的方法。

在制造二项分布概率的参考表格时，通常表格中只填上n/2个值。这是因为k > n/2时的概率可以从它的补集计算出：

${\displaystyle f(k;n,p)=f(n-k;n,1-p)\,}$

因此，我们要看另外一个k和另外一个p（二项分布一般不是对称的）。然而，它的表现不是任意的。总存在一个整数M，满足:

${\displaystyle (n+1)p-1<M\leq (n+1)p\,}$

作为k的函数，表达式ƒ(k ; n, p)当k < M时单调递增，k > M时单调递减，只有当(n + 1)p是整数时例外。在这时，有两个值使ƒ达到最大：(n + 1)p和(n + 1)p − 1。M是伯努利试验的最可能的结果，称为众数。注意它发生的概率可以很小。

累积分布函数可以表示为：

${\displaystyle F(x;n,p)=\Pr(X\leq x)=\sum _{i=0}^{\lfloor x\rfloor }{n \choose i}p^{i}(1-p)^{n-i}}$

其中${\displaystyle \scriptstyle \lfloor x\rfloor \,}$是小于或等于x的最大整数。

它也可以用正则化不完全贝塔函数来表示：

${\displaystyle {\begin{aligned}F(k;n,p)&=\Pr(X\leq k)=I_{1-p}(n-k,k+1)\\&=(n-k){n \choose k}\int _{0}^{1-p}t^{n-k-1}(1-t)^{k}\,dt\end{aligned}}}$

如果X ~ B(n, p)和Y ~ B(m, p)，且X和Y相互独立，那么X + Y也服从二项分布；它的分布为

${\displaystyle X+Y\sim B(n+m,p).\,}$

伯努利分布是二项分布在n = 1时的特殊情况。X ~ B(1, p)与X ~ Bern(p)的意思是相同的。相反，任何二项分布B(n,p)都是n次独立伯努利试验的和，每次试验成功的概率为p。

二项分布是泊松二项分布的一个特殊情况。泊松二项分布是n次独立、不相同的伯努利试验(p_i)的和。如果X服从泊松二项分布，且p₁ = … = p_n =p，那么X ~ B(n, p)。

n=6、p=0.5时的二项分布以及正态近似

如果n足够大，那么分布的偏度就比较小。在这种情况下，如果使用适当的连续性校正，那么B(n, p)的一个很好的近似是正态分布：

${\displaystyle {\mathcal {N}}(np,\,np(1-p))}$

n越大（至少30），近似越好，当p不接近0或1时更好。[5]不同的经验法则可以用来决定n是否足够大，以及p是否距离0或1足够远：

• 一个规则是np和n(1 − p)都必须大于5。

当试验的次数趋于无穷大，而乘积np固定时，二项分布收敛于泊松分布。因此参数为λ = np的泊松分布可以作为二项分布B(n, p)的近似，如果n足够大，而p足够小。[6]