四階八邊形鑲嵌
在幾何學中,四階八邊形鑲嵌是由八邊形組成的雙曲面正鑲嵌圖,在施萊夫利符號中用{8,4}表示。四階八邊形鑲嵌每個頂點皆由四個八邊形共用,且八邊形不重疊,這樣一來,該點處的內角和將超過360度,因此無法存於平面上,但可以在雙曲面上作出。
| 四階八邊形鑲嵌 | |
|---|---|
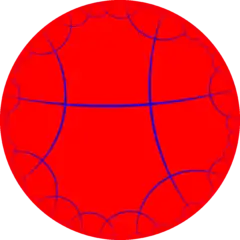 龐加萊圓盤模型 | |
| 類別 | 雙曲正鑲嵌 |
| 頂點圖 | 84 |
| 考克斯特符號 | |
| 施萊夫利符號 | {8,4} r{8,8} |
| 威佐夫符號 | 8 2 |
| 對稱群 | [8,4], (*842) [8,8], (*882) |
| 對偶 | 八階正方形鑲嵌 |
| 旋轉對稱群 | [8,4]+, (842) |
| 特性 | Vertex-transitive、 edge-transitive、 face-transitive |
 八階正方形鑲嵌 (對偶多面體) | |
均勻構造
該鑲嵌有四種均勻構造,其中三種是透過從[8,8]萬花筒中移除鏡射線而形成的。 在二階以及四階頂點間移除鏡射線 [8,8,1+],會成為[(8,8,4)], (*884)對稱性。 在[8,4*]中移除兩條鏡射線,剩餘的鏡射線則為*4444對稱性。
| 均勻塗色 |  |
 |
 |
 |
|---|---|---|---|---|
| 對稱性 | [8,4] (*842) |
[8,8] (*882) |
[(8,4,8)] = [8,8,1+] (*884)
|
[1+,8,8,1+] (*4444) |
| 圖示 | {8,4} | r{8,8} | r(8,4,8) = r{8,8}1⁄2 | r{8,4}1⁄8 = r{8,8}1⁄4 |
| 考斯特圖 |
|
對稱性
可表示以正六邊形的八邊鏡射的雙曲萬花筒。 這種由八個二階交叉反射的對稱性在軌形符號被稱為(*22222222)或著(*28)。 在考斯特表示法可表示為[8*,4], 從三個的鏡射線當中移除兩條穿過八邊形中心的鏡射線。 在原本六邊形基礎中對所有的兩個頂點加入中垂線則可以限定出一個偏方面體44222對稱群;加入對角線則可以限定出一個*444對稱群;加入中垂線則可以限定出一個*4222對稱群;全部加入則限定出了一個*842對稱群。
 *444 |
 *4222 |
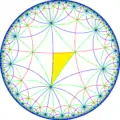 *832 |
該鑲嵌有一種表面塗色,即將八邊形交錯塗上不同顏色。該表面塗色的圖形可以用t1{8,8}的施萊夫利符號表示,是一種半正鑲嵌,稱為截半八階八邊形鑲嵌
 |
 |
相關多面體與鑲嵌
該鑲嵌在拓撲學中和每個面皆為八邊形的多面體及鑲嵌相關, 從正八邊形鑲嵌,施萊夫利符號皆為{8,n},而考斯特符號為![]()
![]()
![]()
![]()
![]() ,從n到無窮。
,從n到無窮。
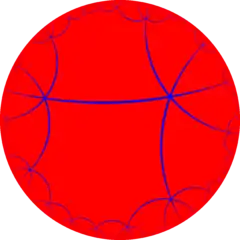
| 球面 | 雙曲鑲嵌 | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
| 8.8 | 83 | 84 | 85 | 86 | 87 | 88 | ...8∞ |
該鑲嵌在拓樸學中也和每個頂點有著四個面的多面體及鑲嵌相關,由正八面體開始, 施萊夫利符號皆為{n,4},而考斯特符號為![]()
![]()
![]()
![]()
![]() ,從n到無窮。
,從n到無窮。
| 球面鑲嵌 | 多面體 | 雙曲鑲嵌 | |||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 | |
| 24 | 34 | 44 | 54 | 64 | 74 | 84 | ...∞4 |
 {3,4} |
 {4,4} |
 {5,4} |
 {6,4} |
 {7,4} |
 {8,4} |
... |  {∞,4} |
參考資料
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- . . Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
