非线性回归

在统计学中， 非线性回归是回归分析的一种形式，其中观测数据由函数建模，该函数是模型参数的非线性组合并且取决于一个或多个独立变量。通过逐次逼近的方法拟合数据。

一般

在非线性回归中，形式的统计模型，

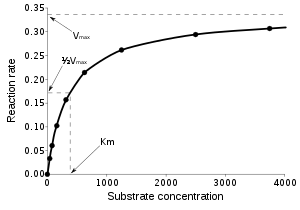
\mathbf {y} \sim f(\mathbf {x} ,{\boldsymbol {\beta }})

关联自变量 x的向量及其相关的观察到的因变量 y 。函数f在参数β的矢量的分量中是非线性的，但在其他方面是任意的。例如，酶动力学的米-门二氏动力学模型有两个参数和一个独立变量，由f相关： [lower-alpha 1]

f(x,{\boldsymbol {\beta }})={\frac {\beta _{1}x}{\beta _{2}+x}}

此函数是非线性的，因为它不能表示为两个 $\beta$ 的线性组合。

系统误差可能存在于自变量中，但其处理不在回归分析的范围内。如果自变量不是无差错的，那么这是一个变量误差模型，也在此范围之外。

非线性函数的其他示例包括指数函数，对数函数，三角函数，幂函数，高斯函数和洛伦兹曲线。某些函数（如指数函数或对数函数）可以进行转换，以使它们是线性的。如此转换，可以执行标准线性回归，但必须谨慎应用。有关详细信息，请参阅下面的线性化§Transformation 。

通常，对于最佳拟合参数，没有闭合形式表达式，如线性回归中所示。通常应用数值优化算法来确定最佳拟合参数。与线性回归相比，可能存在要优化的函数的许多局部最小值，甚至全局最小值也可能产生偏差估计。在实践中，结合优化算法使用参数的估计值来尝试找到平方和的全局最小值。

回归统计

这个过程的基本假设是模型可以用线性函数近似，即一阶泰勒级数：

f(x_{i},{\boldsymbol {\beta }})\approx f(x_{i},0)+\sum _{j}J_{ij}\beta _{j}

其中 $J_{ij}={\frac {\partial f(x_{i},{\boldsymbol {\beta }})}{\partial \beta _{j}}}$ ,由此得出最小二乘估计量由下式给出 .

{\hat {\boldsymbol {\beta }}}\approx \mathbf {(J^{T}J)^{-1}J^{T}y} .

计算非线性回归统计量并将其用作线性回归统计量，但在公式中使用J代替X. 线性近似将偏差引入统计中。因此，在解释从非线性模型得到的统计数据时，需要比平常更多的谨慎。

普通和加权最小二乘法

最佳拟合曲线通常假定应该看起来平方的总和最小化残差。这是普通的最小二乘（OLS）方法。然而，在因变量不具有恒定方差的情况下，可以最小化加权平方残差的总和;看加权最小二乘法。理想情况下，每个权重应等于观察方差的倒数，但是在迭代加权最小二乘算法中，可以在每次迭代时重新计算权重。

线性化

转型

通过模型公式的适当变换，可以将一些非线性回归问题移动到线性域。

例如，考虑非线性回归问题

y=ae^{bx}U\,\!

带有参数a和b以及乘法误差项U.如果我们采用双方的对数，那就变成了

\ln {(y)}=\ln {(a)}+bx+u,\,\!

其中u = ln（ U ），建议通过x上的ln（ y ）的线性回归估计未知参数，该计算不需要迭代优化。但是，使用非线性变换需要谨慎。数据值的影响将发生变化，模型的误差结构和任何推论结果的解释也将发生变化。这些可能不是期望的效果。另一方面，取决于最大误差源是什么，非线性变换可以以高斯方式分布误差，因此必须通过建模考虑来选择执行非线性变换。

对于米-门二氏动力学，线性双倒数图

{\frac {1}{v}}={\frac {1}{V_{\max }}}+{\frac {K_{m}}{V_{\max }[S]}}

1 / v对1 / [ S ]已被大量使用。但是，由于它对数据错误非常敏感，并且强烈偏向于将数据拟合到自变量[ S ]的特定范围内，因此强烈建议不要使用它。

对于属于指数族的误差分布，可以使用链接函数来变换广义线性模型框架下的参数。

分割

芥菜和土壤盐分的产量

独立或解释变量 （比如X）可以分成类或段，并且可以对每个段执行线性回归。具有置信度分析的分段回归可以产生依赖或响应变量（假设Y）在各个段中表现不同的结果。 [1]

该图显示土壤盐度（X）最初对芥菜的作物产量（Y）没有影响，直到临界值或阈值（断点），之后产量受到负面影响。 [2]

参见

方差分析
安斯库姆四重奏
横截面回归
曲线拟合
经验贝叶斯方法
逻辑斯蒂回归
M估计
非线性回归
非参数回归
多元自适应回归样条
Lack-of-fit sum of squares
截断回归模型
删失回归模型
简单线性回归
分段线性回归

非线性最小二乘法
曲线拟合
广义线性模型
局部回归

RJOosterbaan，1994，频率和回归分析。在：HPRitzema（ed。），Drainage Principles and Applications，Publ。 16，pp.175-224，国际土地复垦与改良研究所（ILRI），荷兰瓦赫宁根。
RJOosterbaan，2002年。农民田间的排水研究：数据分析。国际土地复垦与改良研究所（ILRI）项目“液体黄金”的一部分，荷兰瓦赫宁根。以PDF格式下载：。这个数字是用SegReg程序制作的，可以从免费下载。

脚注

This model can also be expressed in the conventional biological notation:
$v={\frac {V_{\max }\ [{\mbox{S}}]}{K_{m}+[{\mbox{S}}]}}$

拓展阅读

Bethea, R. M.; Duran, B. S.; Boullion, T. L. . New York: Marcel Dekker. 1985. ISBN 0-8247-7227-X.
Meade, N.; Islam, T. . Journal of Forecasting. 1995, 14 (5): 413–430. doi:10.1002/for.3980140502.
Schittkowski, K. . Boston: Kluwer. 2002. ISBN 1402010796.
Seber, G. A. F.; Wild, C. J. . New York: John Wiley and Sons. 1989. ISBN 0471617601.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[2] RJOosterbaan，1994，频率和回归分析。在：HPRitzema（ed。），Drainage Principles and Applications，Publ。 16，pp.175-224，国际土地复垦与改良研究所（ILRI），荷兰瓦赫宁根。

[3] RJOosterbaan，2002年。农民田间的排水研究：数据分析。国际土地复垦与改良研究所（ILRI）项目“液体黄金”的一部分，荷兰瓦赫宁根。以PDF格式下载：。这个数字是用SegReg程序制作的，可以从免费下载。

[1] This model can also be expressed in the conventional biological notation:
$v={\frac {V_{\max }\ [{\mbox{S}}]}{K_{m}+[{\mbox{S}}]}}$