正割
正割(Secant,)是三角函数的一种。它的定义域不是整个实数集,值域是絕對值大於等于一的实数。它是周期函数,其最小正周期为。
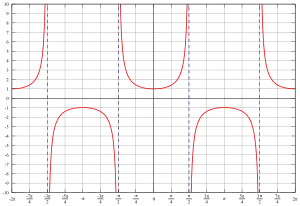 | |
| 性質 | |
| 奇偶性 | 偶 |
| 定義域 | {x|x≠kπ+π/2,k∈Z} |
| 到達域 | |secx|≥1 |
| 周期 | 2π |
| 特定值 | |
| 當x=0 | 1 |
| 當x=+∞ | N/A |
| 當x=-∞ | N/A |
| 最大值 | +∞ |
| 最小值 | -∞ |
| 其他性質 | |
| 渐近线 | N/A |
| 根 | 無實根 |
| 臨界點 | kπ |
| 拐點 | kπ-π/2 |
| k是一個整數。 | |
正割是三角函数的正函數(正弦、正切、正割、正矢)之一,所以在到的區間之間,函數是遞增的,另外正割函数和餘弦函数互為倒數。
在單位圓上,正割函数位於割線上,因此將此函數命名為正割函数。
符号史
正割的数学符号为,出自英文secant。该符号最早由数学家吉拉德在他的著作《三角学》中所用。
定义
单位圆定义
图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线,同x轴正半部分得到一个角,并与单位圆相交。这个交点的y坐标等于。在这个图形中的三角形确保了这个公式;半径等于斜边并有长度1,所以有了。单位圆可以被认为是通过改变邻边和对边的长度并保持斜边等于1查看无限数目的三角形的一种方式。
对于大于或小于的角度,简单的继续绕单位圆旋转。在这种方式下,正割变成了周期为的周期函数:
对于任何角度和任何整数。
級數定義
正割也能使用泰勒級數來定義:
- 。
微分方程定義
指數定義
恆等式
和差角公式
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.


