佩尔数

佩尔数由以下的递推关系定义：

${\displaystyle P_{n}={\begin{cases}0&{\mbox{if }}n=0;\\1&{\mbox{if }}n=1;\\2P_{n-1}+P_{n-2}&{\mbox{otherwise.}}\end{cases}}}$

也就是说，佩尔数的数列从0和1开始，以后每一个佩尔数都是前面的数的两倍加上再前面的数。最初几个佩尔数是：

0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378…… （OEIS中的数列A000129）。

佩尔数也可以用通项公式来定义：

${\displaystyle P_{n}={\frac {(1+{\sqrt {2}})^{n}-(1-{\sqrt {2}})^{n}}{2{\sqrt {2}}}}.}$

对于较大的n，${\displaystyle \scriptstyle (1+{\sqrt {2}})^{n}}$的项起主要作用，而${\displaystyle \scriptstyle (1-{\sqrt {2}})^{n}}$的项则变得微乎其微。因此佩尔数大约与白银比${\displaystyle \scriptstyle (1+{\sqrt {2}})}$的幂成正比。

第三种定义是以下的矩阵公式：

${\displaystyle {\begin{pmatrix}P_{n+1}&P_{n}\\P_{n}&P_{n-1}\end{pmatrix}}={\begin{pmatrix}2&1\\1&0\end{pmatrix}}^{n}.}$

从这些定义中，可以推出或证明许多恒等式；例如以下的恒等式，与斐波那契数的卡西尼恒等式类似：

${\displaystyle P_{n+1}P_{n-1}-P_{n}^{2}=(-1)^{n},}$

这个恒等式是以上矩阵公式的直接结果（考虑矩阵的行列式）。

佩尔数出现在2的算術平方根的有理数近似值中。如果两个大的整数x和y 是佩尔方程的解：

${\displaystyle \displaystyle x^{2}-2y^{2}=\pm 1,}$

那么它们的比${\displaystyle {\tfrac {x}{y}}}$就是${\displaystyle \scriptstyle {\sqrt {2}}}$的一个较精确的近似值。这种形式的近似值的数列是：

${\displaystyle 1,{\frac {3}{2}},{\frac {7}{5}},{\frac {17}{12}},{\frac {41}{29}},{\frac {99}{70}},\dots }$

其中每一个分数的分母是佩尔数，分子则是这个数与前一个佩尔数的和。也就是说，佩尔方程的解具有${\displaystyle {\tfrac {P_{n-1}+P_{n}}{P_{n}}}}$的形式。${\displaystyle {\sqrt {2}}\approx {\frac {577}{408}}}$是这些近似值中的第八个，在公元前3或4世纪就已经为印度数学家所知。公元前5世纪的古希腊数学家也知道这个近似值的数列；他们把这个数列的分母和分子称为“边长和直径数”，分子也称为“有理对角线”或“有理直径”。

这些近似值可以从${\displaystyle \scriptstyle {\sqrt {2}}}$的连分数展开式推出：

${\displaystyle {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{\ddots \,}}}}}}}}}}.}$

取这个展开式的有限个项，便可以产生${\displaystyle \scriptstyle {\sqrt {2}}}$的一个近似值，例如：

${\displaystyle {\frac {577}{408}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2}}}}}}}}}}}}}}.}$

佩尔素数是既是佩尔数又是素数的数。最初几个佩尔素数是：

2, 5, 29, 5741, …… （OEIS中的数列A086383）。

与斐波那契素数相似，仅当n本身是素数时${\displaystyle P_{n}}$才有可能是素数。

唯一的既是佩尔数又是平方数、立方数或任意整数次方的数是0, 1, 以及169 = 13²。

然而，佩尔数与三角平方数有密切的关系。它们出现在以下佩尔数的恒等式中：

${\displaystyle {\bigl (}(P_{k-1}+P_{k})\cdot P_{k}{\bigr )}^{2}={\frac {(P_{k-1}+P_{k})^{2}\cdot \left((P_{k-1}+P_{k})^{2}-(-1)^{k}\right)}{2}}.}$

等式的左面是平方数，等式的右面是三角形数，因此是三角平方数。

Santana和Diaz-Barrero在2006年证明了佩尔数与平方数之间的另外一个恒等式，并证明了从${\displaystyle P_{1}}$到${\displaystyle P_{4n+1}}$的所有佩尔数的和总是平方数：

${\displaystyle \sum _{i=0}^{4n+1}P_{i}=\left(\sum _{r=0}^{n}2^{r}{2n+1 \choose 2r}\right)^{2}=(P_{2n}+P_{2n+1})^{2}.}$

例如，从${\displaystyle P_{1}}$到${\displaystyle P_{5}}$的和是${\displaystyle 0+1+2+5+12+29=49}$，是${\displaystyle P_{2}+P_{3}=2+5=7}$的平方。${\displaystyle P_{2n}+P_{2n+1}}$就是这个和的平方根：

1, 7, 41, 239, 1393, 8119, 47321, …… （OEIS中的数列A002315）。

边长为整数的直角三角形，其直角边几乎相等，由佩尔数引出。

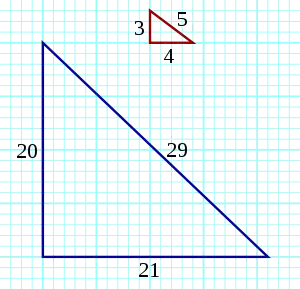
如果一个直角三角形的边长为a、b和c（必须满足勾股定理a²+b²=c²），那么(a,b,c)称为勾股数。Martin在1875年描述，佩尔数可以用来产生勾股数，其中a和b相差一个单位。这个勾股数具有以下形式：

${\displaystyle (2P_{n}P_{n+1},P_{n+1}^{2}-P_{n}^{2},P_{n+1}^{2}+P_{n}^{2}=P_{2n+1}).}$

用这种方法产生的勾股数的序列是：

(4,3,5), (20,21,29), (120,119,169), (696,697,985), ……

佩尔-卢卡斯数由以下的递推关系定义：

${\displaystyle Q_{n}={\begin{cases}2&{\mbox{if }}n=0;\\2&{\mbox{if }}n=1;\\2Q_{n-1}+Q_{n-2}&{\mbox{otherwise.}}\end{cases}}}$

也就是说，数列中的最初两个数都是2，后面每一个数都是前一个数的两倍加上再前面的一个数。这个数列的最初几个项是（OEIS中的数列A002203）：2, 2, 6, 14, 34, 82, 198, 478……

佩尔-卢卡斯数的通项公式为：

${\displaystyle Q_{n}=(1+{\sqrt {2}})^{n}+(1-{\sqrt {2}})^{n}.}$

这些数都是偶数，每一个数都是以上${\displaystyle \scriptstyle {\sqrt {2}}}$的近似值中的分子的两倍。

• 埃里克·韦斯坦因. . MathWorld.