廣義相對論中的數學入門
廣義相對論所使用的數學很複雜。牛頓的運動理論中,物體做加速度運動時,其長度和時間流逝的速率保持定值,這表示牛頓力學中的許多問題用代數就能解決。然而,相對論中的物體在運動速度接近光速時,長度和時間流逝的速率會有可觀的改變,這表示要計算物體的運動必須用上更多變數和複雜的數學,如向量、張量、偽張量、曲線座標等概念。
| 廣義相對論 |
|---|
 |
|
解
|
向量與張量
向量

在數學、物理學及工程學中,歐幾里得向量(有時也稱為「幾何向量」[1]、「空間向量」[2],或單稱「向量」)是同時有量值(長度)和方向的幾何對象。一個向量將點「搬運」至點;向量的拉丁文「vector」意思為「搬運東西的東西」。[3]向量的量值就是兩點之間的距離,方向則為到的位移方向。很多實數的代數運算,像加、減、乘、邏輯非,和向量的運算很類似,運算也遵守相似的代數法則,如交換律、結合律、分配律。
張量

張量將向量的概念延伸至額外的維度。純量是沒有方向的量,是單純的數字,在圖上以點來表示,是零維的物件。向量則有量值和方向,在圖上以線呈現,是一維的物件。張量延伸了向量的概念,一個二維的張量稱為二階張量,可以看成一組相關的向量,在一個平面上的多個方向移動。
應用
向量在物理科學裡很基礎。他們可用來代表所有同時有量值和方向的量,例如速度。速度的量值為速率。舉例而言,每秒五公尺向上的速度可以向量(0, 5)表示(在二維以軸的正方向表示向上)。力的量也能以向量表示,因為它有量值和方向。向量也能描述很多其他的物理量,如位移、加速度、動量和角動量。其他物理向量,如電場和磁場,以物理空間中所有點的向量系統表示,也就是向量場。
張量在物理中也有延伸應用:
座標轉換


In physics, as well as mathematics, a vector is often identified with a tuple, or list of numbers, which depend on some auxiliary coordinate system or reference frame. When the coordinates are transformed, for example by rotation or stretching of the coordinate system, then the components of the vector also transform. The vector itself has not changed, but the reference frame has, so the components of the vector (or measurements taken with respect to the reference frame) must change to compensate.
The vector is called covariant or contravariant depending on how the transformation of the vector's components is related to the transformation of coordinates.
- Contravariant vectors are "regular vectors" with units of distance (such as a displacement) or distance times some other unit (such as velocity or acceleration). For example, in changing units from meters to millimeters, a displacement of 1 m becomes 1000 mm.
- Covariant vectors, on the other hand, have units of one-over-distance (typically such as gradient). For example, in changing again from meters to millimeters, a gradient of 1 K/m becomes 0.001 K/mm.
In Einstein notation, contravariant vectors and components of tensors are shown with superscripts, e.g. xi, and covariant vectors and components of tensors with subscripts, e.g. xi. Indices are "raised" or "lowered" by multiplication by an appropriate matrix, often the identity matrix.
Coordinate transformation is important because relativity states that there is no one correct reference point in the universe. On earth, we use dimensions like north, east, and elevation, which are used throughout the entire planet. There is no such system for space. Without a clear reference grid, it becomes more accurate to describe the four dimensions as towards/away, left/right, up/down and past/future. As an example event, take the signing of the Declaration of Independence. To a modern observer on Mount Rainier looking east, the event is ahead, to the right, below, and in the past. However, to an observer in medieval England looking north, the event is behind, to the left, neither up nor down, and in the future. The event itself has not changed, the location of the observer has.
斜軸
An oblique coordinate system is one in which the axes are not necessarily orthogonal to each other; that is, they meet at angles other than right angles. When using coordinate transformations as described above, the new coordinate system will often appear to have oblique axes compared to the old system.
非張量
A nontensor is a tensor-like quantity that behaves like a tensor in the raising and lowering of indices, but that does not transform like a tensor under a coordinate transformation. For example, Christoffel symbols cannot be tensors themselves if the coordinates don't change in a linear way.
In general relativity, one cannot describe the energy and momentum of the gravitational field by an energy–momentum tensor. Instead, one introduces objects that behave as tensors only with respect to restricted coordinate transformations. Strictly speaking, such objects are not tensors at all. A famous example of such a pseudotensor is the Landau–Lifshitz pseudotensor.
曲線座標和彎曲時空
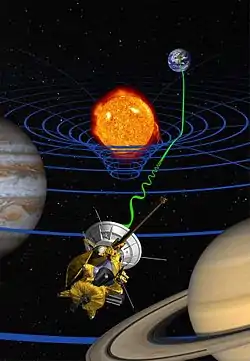
Curvilinear coordinates are coordinates in which the angles between axes can change from point to point. This means that rather than having a grid of straight lines, the grid instead has curvature.
A good example of this is the surface of the Earth. While maps frequently portray north, south, east and west as a simple square grid, that is not in fact the case. Instead, the longitude lines running north and south are curved and meet at the north pole. This is because the Earth is not flat, but instead round.
In general relativity, gravity has curvature effects on the four dimensions of the universe. A common analogy is placing a heavy object on a stretched out rubber sheet, causing the sheet to bend downward. This curves the coordinate system around the object, much like an object in the universe curves the coordinate system it sits in. The mathematics here are conceptually more complex than on Earth, as it results in four dimensions of curved coordinates instead of three as used to describe a curved 2D surface.
平行移動

高維空間中的區間
In a Euclidean space, the separation between two points is measured by the distance between the two points. The distance is purely spatial, and is always positive. In spacetime, the separation between two events is measured by the invariant interval between the two events, which takes into account not only the spatial separation between the events, but also their temporal separation. The interval, s2, between two events is defined as:
- (spacetime interval),
where c is the speed of light, and Δr and Δt denote differences of the space and time coordinates, respectively, between the events. The choice of signs for s2 above follows the space-like convention (−+++). A notation like Δr2 means (Δr)2. The reason s2 is called the interval and not s is that s2 can be positive, zero or negative.
Spacetime intervals may be classified into three distinct types, based on whether the temporal separation (c2Δt2) or the spatial separation (Δr2) of the two events is greater: time-like, light-like or space-like.
Certain types of world lines are called geodesics of the spacetime – straight lines in the case of Minkowski space and their closest equivalent in the curved spacetime of general relativity. In the case of purely time-like paths, geodesics are (locally) the paths of greatest separation (spacetime interval) as measured along the path between two events, whereas in Euclidean space and Riemannian manifolds, geodesics are paths of shortest distance between two points.[4][5] The concept of geodesics becomes central in general relativity, since geodesic motion may be thought of as "pure motion" (inertial motion) in spacetime, that is, free from any external influences.
協變導數
The covariant derivative is a generalization of the directional derivative from vector calculus. As with the directional derivative, the covariant derivative is a rule, which takes as its inputs: (1) a vector, u, (along which the derivative is taken) defined at a point P, and (2) a vector field, v, defined in a neighborhood of P. The output is a vector, also at the point P. The primary difference from the usual directional derivative is that the covariant derivative must, in a certain precise sense, be independent of the manner in which it is expressed in a coordinate system.
平行移動
Given the covariant derivative, one can define the parallel transport of a vector v at a point P along a curve γ starting at P. For each point x of γ, the parallel transport of v at x will be a function of x, and can be written as v(x), where v(0) = v. The function v is determined by the requirement that the covariant derivative of v(x) along γ is 0. This is similar to the fact that a constant function is one whose derivative is constantly 0.
克里斯多福符號
The equation for the covariant derivative can be written in terms of Christoffel symbols. The Christoffel symbols find frequent use in Einstein's theory of general relativity, where spacetime is represented by a curved 4-dimensional Lorentz manifold with a Levi-Civita connection. The Einstein field equations – which determine the geometry of spacetime in the presence of matter – contain the Ricci tensor. Since the Ricci tensor is derived from the Riemann tensor, which can be written in terms of Christoffel symbols, a calculation of the Christoffel symbols is essential. Once the geometry is determined, the paths of particles and light beams are calculated by solving the geodesic equations in which the Christoffel symbols explicitly appear.
測地線
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational force, is a particular type of geodesic. In other words, a freely moving or falling particle always moves along a geodesic.
In general relativity, gravity can be regarded as not a force but a consequence of a curved spacetime geometry where the source of curvature is the stress–energy tensor (representing matter, for instance). Thus, for example, the path of a planet orbiting around a star is the projection of a geodesic of the curved 4-dimensional spacetime geometry around the star onto 3-dimensional space.
A curve is a geodesic if the tangent vector of the curve at any point is equal to the parallel transport of the tangent vector of the base point.
曲率張量
The Riemann tensor tells us, mathematically, how much curvature there is in any given region of space. Contracting the tensor produces 3 different mathematical objects:
- The Riemann curvature tensor: Rρσμν, which gives the most information on the curvature of a space and is derived from derivatives of the metric tensor. In flat space this tensor is zero.
- The Ricci tensor: Rσν, comes from the need in Einstein's theory for a curvature tensor with only 2 indices. It is obtained by averaging certain portions of the Riemann curvature tensor.
- The scalar curvature: R, the simplest measure of curvature, assigns a single scalar value to each point in a space. It is obtained by averaging the Ricci tensor.
The Riemann curvature tensor can be expressed in terms of the covariant derivative.
The Einstein tensor G is a rank-2 tensor defined over pseudo-Riemannian manifolds. In index-free notation it is defined as
where R is the Ricci tensor, g is the metric tensor and R is the scalar curvature. It is used in the Einstein field equations.
應力-能量張量

The stress–energy tensor (sometimes stress–energy–momentum tensor or energy–momentum tensor) is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields. The stress–energy tensor is the source of the gravitational field in the Einstein field equations of general relativity, just as mass density is the source of such a field in Newtonian gravity.
愛因斯坦方程
The Einstein field equations (EFE) or Einstein's equations are a set of 10 equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy.[6] First published by Einstein in 1915[7] as a tensor equation, the EFE equate local spacetime curvature (expressed by the Einstein tensor) with the local energy and momentum within that spacetime (expressed by the stress–energy tensor).[8]
The Einstein Field Equations can be written as
where Gμν is the Einstein tensor and Tμν is the stress–energy tensor.
This implies that the curvature of space (represented by the Einstein tensor) is directly connected to the presence of matter and energy (represented by the stress–energy tensor).
史瓦西解與黑洞
In Einstein's theory of general relativity, the Schwarzschild metric (also Schwarzschild vacuum or Schwarzschild solution), is a solution to the Einstein field equations which describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, the angular momentum of the mass, and the universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. The solution is named after Karl Schwarzschild, who first published the solution in 1916.
According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric, vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has no charge or angular momentum. A Schwarzschild black hole is described by the Schwarzschild metric, and cannot be distinguished from any other Schwarzschild black hole except by its mass.
註釋
- Ivanov 2001
- Heinbockel 2001
- From Latin vectus, perfect participle of vehere, "to carry". For historical development of the word vector, see . 牛津英語詞典 (第三版). 牛津大學出版社. 2005-09 (英语). and Jeff Miller. . [2007-05-25].
- This characterization is not universal: both the arcs between two points of a great circle on a sphere are geodesics.
- Berry, Michael V. . CRC Press. 1989: 58. ISBN 0-85274-037-9. Extract of page 58, caption of Fig. 25
- Einstein, Albert. . Annalen der Physik. 1916, 354 (7): 769. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702. (原始内容 (PDF)存档于2006-08-29).
- Einstein, Albert. . Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin. November 25, 1915: 844–847 [2006-09-12].
- Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald. . San Francisco: W. H. Freeman. 1973. ISBN 978-0-7167-0344-0. Chapter 34, p 916
參考文獻
- P. A. M. Dirac. . Princeton University Press. 1996. ISBN 0-691-01146-X.
- Misner, Charles; Thorne, Kip S.; Wheeler, John Archibald. . San Francisco: W. H. Freeman. 1973. ISBN 0-7167-0344-0.
- Landau, L. D.; Lifshitz, E. M. . Oxford: Pergamon. 1975. ISBN 0-08-018176-7.
- R. P. Feynman; F. B. Moringo; W. G. Wagner. . Addison-Wesley. 1995. ISBN 0-201-62734-5.
- Einstein, A. . New York: Crown. 1961. ISBN 0-517-02961-8.
