斐波那契数列

（意大利语：Successione di Fibonacci），又譯為菲波拿契數列、菲波那西數列、斐氏數列、黃金分割數列。

以斐波那契數為邊的正方形拼成的近似的黃金矩形(1:1.618)

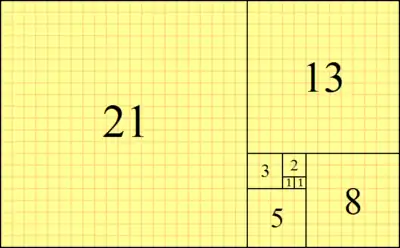
在數學上，斐波那契數列是以遞歸的方法來定義：

$F_{0}=0$
$F_{1}=1$
$F_{n}=F_{n-1}+F_{n-2}$ （n≧2）

用文字來說，就是斐波那契數列由0和1開始，之後的斐波那契數就是由之前的兩數相加而得出。首幾個斐波那契數是：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……（OEIS中的数列A000045）

特別指出：0不是第一項，而是第零項。

源起

公元1150年印度數學家Gopala和金月在研究箱子包裝物件長宽剛好為1和2的可行方法數目時，首先描述這個數列。在西方，最先研究這個數列的人是比薩的李奧納多（義大利人斐波那契Leonardo Fibonacci），他描述兔子生長的數目時用上了這數列:

兔子对的数量就是斐波那契数列

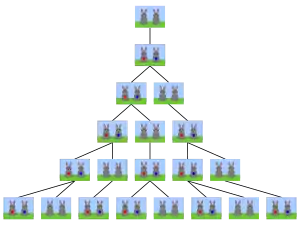
第一個月初有一對剛誕生的兔子
第二個月之後（第三個月初）牠們可以生育
每月每對可生育的兔子會誕生下一對新兔子
兔子永不死去

假設在n月有兔子總共a對，n+1月總共有b對。在n+2月必定總共有a+b對：因為在n+2月的時候，前一月（n+1月）的b對兔子可以存留至第n+2月（在當月屬於新誕生的兔子尚不能生育）。而新生育出的兔子對數等於所有在n月就已存在的a對

斐波纳契数是帕斯卡三角形的每一条红色对角线上数字的和。

斐波纳契数也是帕斯卡三角形的每一条红色对角线上数字的和。

表達式

為求得斐波那契數列的一般表達式，可以藉助線性代數的方法。高中的初等數學知識也能求出。

初等代數解法

已知

$a_{1}=1$
$a_{2}=1$
$a_{n}=a_{n-1}+a_{n-2}$

首先構建等比數列

設 $a_{n}+\alpha a_{n-1}=\beta (a_{n-1}+\alpha a_{n-2})$
化簡得
$a_{n}=(\beta -\alpha )a_{n-1}+\alpha \beta a_{n-2}$
比較係數可得：
${\begin{cases}\beta -\alpha =1\\\alpha \beta =1\end{cases}}$
不妨設 $\beta >0,\alpha >0$
解得：

${\begin{cases}\alpha ={\dfrac {{\sqrt {5}}-1}{2}}\\\beta ={\dfrac {{\sqrt {5}}+1}{2}}\end{cases}}$
又因为有 $a_{n}+\alpha a_{n-1}=\beta (a_{n-1}+\alpha a_{n-2})$ ，即 $\left\{a_{n}+\alpha a_{n-1}\right\}$ 為等比數列。

求出數列{ $a_{n}+\alpha a_{n-1}$ }

由以上可得：
${\begin{aligned}a_{n+1}+\alpha a_{n}&=(a_{2}+\alpha a_{1})\beta ^{n-1}\\&=(1+\alpha )\beta ^{n-1}\\&=\beta ^{n}\\\end{aligned}}$

變形得： ${\frac {a_{n+1}}{\beta ^{n+1}}}+{\frac {\alpha }{\beta }}\cdot {\frac {a_{n}}{\beta ^{n}}}={\frac {1}{\beta }}$ 。令 $b_{n}={\frac {a_{n}}{\beta ^{n}}}$

求數列{ $b_{n}$ }進而得到{ $a_{n}$ }

$b_{n+1}+{\frac {\alpha }{\beta }}b_{n}={\frac {1}{\beta }}$
設 $b_{n+1}+\lambda =-{\frac {\alpha }{\beta }}(b_{n}+\lambda )$ ，解得 $\lambda =-{\frac {1}{\alpha +\beta }}$ 。故數列 $\left\{b_{n}+\lambda \right\}$ 為等比數列
即 $b_{n}+\lambda =\left(-{\frac {\alpha }{\beta }}\right)^{n-1}\left(b_{1}+\lambda \right)$ 。而 $b_{1}={\frac {a_{1}}{\beta }}={\frac {1}{\beta }}$ ，故有 $b_{n}+\lambda =\left(-{\frac {\alpha }{\beta }}\right)^{n-1}\left({\frac {1}{\beta }}+\lambda \right)$
又有 ${\begin{cases}\alpha ={\dfrac {{\sqrt {5}}-1}{2}}\\\beta ={\dfrac {{\sqrt {5}}+1}{2}}\end{cases}}$ 和 $b_{n}={\frac {a_{n}}{\beta ^{n}}}$
可得 $a_{n}={\frac {\sqrt {5}}{5}}\cdot \left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right]$

得出 ${a_{n}}$ 表達式

$a_{n}={\frac {\sqrt {5}}{5}}\cdot \left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right]$

線性代數解法

${\begin{pmatrix}F_{n+2}\\F_{n+1}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}\cdot {\begin{pmatrix}F_{n+1}\\F_{n}\end{pmatrix}}$

${\begin{pmatrix}F_{n+2}&F_{n+1}\\F_{n+1}&F_{n}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}^{n+1}$

構建一個矩陣方程

設J_n為第n個月有生育能力的兔子數量，A_n為這一月份的兔子數量。

{J_{n+1} \choose A_{n+1}}={\begin{pmatrix}0&1\\1&1\end{pmatrix}}\cdot {J_{n} \choose A_{n}},

上式表達了兩個月之間，兔子數目之間的關係。而要求的是，A_n+1的表達式。

求矩陣的特徵值： $\lambda$

行列式： $-\lambda (1-\lambda )-1\times 1=\lambda ^{2}-\lambda -1$

當行列式的值為0，解得 $\lambda _{1}$ = ${\frac {1}{2}}(1+{\sqrt {5}})$ 或 $\lambda _{2}$ = ${\frac {1}{2}}(1-{\sqrt {5}})$

特徵向量

將兩個特徵值代入

({\begin{pmatrix}0&1\\1&1\end{pmatrix}}-\lambda \cdot E)\cdot {\vec {x}}=0

求特徵向量 ${\vec {x}}$ 得

${\vec {x}}_{1}$ = ${\begin{pmatrix}1\\{\frac {1}{2}}(1+{\sqrt {5}})\end{pmatrix}}$

${\vec {x}}_{2}$ = ${\begin{pmatrix}1\\{\frac {1}{2}}(1-{\sqrt {5}})\end{pmatrix}}$

分解首向量

第一個月的情況是兔子一對，新生0對。

{J_{1} \choose A_{1}}={\begin{pmatrix}0\\1\end{pmatrix}}

將它分解為用特徵向量表示。

{\begin{pmatrix}0\\1\end{pmatrix}}={\frac {1}{\sqrt {5}}}\cdot {\begin{pmatrix}1\\{\frac {1}{2}}(1+{\sqrt {5}})\end{pmatrix}}-{\frac {1}{\sqrt {5}}}\cdot {\begin{pmatrix}1\\{\frac {1}{2}}(1-{\sqrt {5}})\end{pmatrix}}

（4）

用數學歸納法證明

從

{J_{n+1} \choose A_{n+1}}={\begin{pmatrix}0&1\\1&1\end{pmatrix}}\cdot {J_{n} \choose A_{n}}

=

\lambda \cdot {J_{n} \choose A_{n}}

可得到

{J_{n+1} \choose A_{n+1}}={\begin{pmatrix}0&1\\1&1\end{pmatrix}}^{n}\cdot {J_{1} \choose A_{1}}=\lambda ^{n}\cdot {J_{1} \choose A_{1}}

（5）

化簡矩陣方程

將（4）代入（5）

{J_{n+1} \choose A_{n+1}}=\lambda ^{n}\cdot \left[{\frac {1}{\sqrt {5}}}\cdot {\begin{pmatrix}1\\{\frac {1}{2}}(1+{\sqrt {5}})\end{pmatrix}}-{\frac {1}{\sqrt {5}}}\cdot {\begin{pmatrix}1\\{\frac {1}{2}}(1-{\sqrt {5}})\end{pmatrix}}\right]

根據3

{J_{n+1} \choose A_{n+1}}={\frac {1}{\sqrt {5}}}\cdot \lambda _{1}^{n}\cdot {\begin{pmatrix}1\\{\frac {1}{2}}(1+{\sqrt {5}})\end{pmatrix}}-{\frac {1}{\sqrt {5}}}\cdot \lambda _{2}^{n}\cdot {\begin{pmatrix}1\\{\frac {1}{2}}(1-{\sqrt {5}})\end{pmatrix}}

求A的表達式

現在在6的基礎上，可以很快求出A_n+1的表達式，將兩個特徵值代入6中

A_{n+1}={\frac {1}{\sqrt {5}}}\cdot \lambda _{1}^{n+1}-{\frac {1}{\sqrt {5}}}\cdot \lambda _{2}^{n+1}

A_{n+1}={\frac {1}{\sqrt {5}}}\cdot (\lambda _{1}^{n+1}-\lambda _{2}^{n+1})

A_{n+1}={\frac {1}{\sqrt {5}}}\cdot \left\{\left[{\frac {1}{2}}\left(1+{\sqrt {5}}\right)\right]^{n+1}-\left[{\frac {1}{2}}(1-{\sqrt {5}})\right]^{n+1}\right\}

（7）

（7）即為A_n+1的表達式

數論解法

實際上，如果將斐波那契數列的通項公式寫成 $a_{n}-a_{n-1}-a_{n-2}=0$ ，即可利用解二階線性齊次遞迴關係式的方法，寫出其特徵多項式 $\lambda ^{2}-\lambda -1=0$ （該式和表達斐波那契數列的矩陣的特徵多項式一致），然後解出 $\lambda _{1}$ = ${\frac {1}{2}}(1+{\sqrt {5}})$ ， $\lambda _{2}$ = ${\frac {1}{2}}(1-{\sqrt {5}})$ ，即有 $a_{n}=c_{1}\lambda _{1}^{n}+c_{2}\lambda _{2}^{n}$ ，其中 $c_{1},c_{2}$ 为常数。我们知道 $a_{0}=0,a_{1}=1$ ，因此 ${\begin{cases}c_{1}+c_{2}=0\\{\frac {c_{1}(1+{\sqrt {5}})}{2}}+{\frac {c_{2}(1-{\sqrt {5}})}{2}}=1\end{cases}}$ ，解得 $c_{1}={\frac {1}{\sqrt {5}}},c_{2}=-{\frac {1}{\sqrt {5}}}$ 。

組合數解法

$F_{n}=\sum _{i=0}^{\infty }{\binom {n-i}{i}}$ [1]

F_{n-1}+F_{n}=\sum _{i=0}^{\infty }{\binom {n-1-i}{i}}+\sum _{i=0}^{\infty }{\binom {n-i}{i}}=1+\sum _{i=1}^{\infty }{\binom {n-i}{i-1}}+\sum _{i=1}^{\infty }{\binom {n-i}{i}}=1+\sum _{i=1}^{\infty }{\binom {n+1-i}{i}}=\sum _{i=0}^{\infty }{\binom {n+1-i}{i}}=F_{n+1}

近似值

F_{n}\approx {\frac {1}{\sqrt {5}}}a^{n}={\frac {1}{\sqrt {5}}}\cdot \left[{\frac {1}{2}}\left(1+{\sqrt {5}}\right)\right]^{n}\approx 0.4472135955\cdot 1.618033988745^{n}

用計算機求解

可通過編程觀察斐波那契數列。分為兩類問題，一種已知數列中的某一項，求序數。第二種是已知序數，求該項的值。

可通過遞歸遞推的算法解決此兩個問題。事實上當n相當巨大的時候，O（n）的遞推/遞歸非常慢……這時候要用到矩陣快速幂這一技巧，可以使遞迴加速到O(logn)。

和黃金分割的關係

開普勒發現數列前、後兩項之比1/2 ,2/3 , 3/5 ,5/8 ,8/13 ,13/21 ,21/34 ,...... ,也組成了一個數列，會趨近黃金分割：

{\frac {f_{n+1}}{f_{n}}}\approx a={\frac {1}{2}}(1+{\sqrt {5}})=\varphi \approx 1{.}618{...}

斐波那契數亦可以用連分數來表示：

${\frac {1}{1}}=1\qquad {\frac {2}{1}}=1+{\frac {1}{1}}\qquad {\frac {3}{2}}=1+{\frac {1}{1+{\frac {1}{1}}}}\qquad {\frac {5}{3}}=1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1}}}}}}\qquad {\frac {8}{5}}=1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1}}}}}}}}$

$F_{n}={\frac {1}{\sqrt {5}}}\left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right]={\varphi ^{n} \over {\sqrt {5}}}-{(1-\varphi )^{n} \over {\sqrt {5}}}$

而黃金分割數亦可以用無限連分數表示：

\varphi =1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+...}}}}}}}}

而黃金分割數也可以用無限多重根號表示：

\varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+...}}}}}}}}

與平方數的關係

斐波那契数列中，只有3個平方數：0、1、144。[2]

和自然的關係

許多的生物構成都和斐波那契數列有正相關。例如人體從脚底至頭頂之距離和從肚臍至腳底之距趨近於 $\lim _{n\to \infty }{\frac {F_{n}}{F_{(n-1)}}}$ ,向日葵的種子螺旋排列有99%是 $F_{n}$ 。

恆等式

資料來源：[3]

證明以下的恆等式有很多方法。以下會用組合論述來證明。

$F_{n}$ 可以表示用多個1和多個2相加令其和等於 $n$ 的方法的數目。

不失一般性，我們假設 $n\geq 1$ ， $F_{n+1}$ 是計算了將1和2加到n的方法的數目。若第一個被加數是1，有 $F_{n}$ 種方法來完成對 $n-1$ 的計算；若第一個被加數是2，有 $F_{n-1}$ 來完成對 $n-2$ 的計算。因此，共有 $F_{n}+F_{n-1}$ 種方法來計算n的值。

$F_{0}+F_{1}+F_{2}+F_{3}+...+F_{n}=F_{n+2}-1$

計算用多個1和多個2相加令其和等於 $n+1$ 的方法的數目，同時至少一個加數是2的情況。

如前所述，當 $n>0$ ，有 $F_{n+2}$ 種這樣的方法。因為當中只有一種方法不用使用2，就即 $1+1+...+1$ 　（ $n+1$ 項），於是我們從 $F_{n+2}$ 減去1。

若第1個被加數是2，有 $F_{n}$ 種方法來計算加至 $n-1$ 的方法的數目；
若第2個被加數是2、第1個被加數是1，有 $F_{n-1}$ 種方法來計算加至 $n-2$ 的方法的數目。
重複以上動作。
若第 $n+1$ 個被加數為2，它之前的被加數均為1，就有 $F_{0}$ 種方法來計算加至0的數目。

若該數式包含2為被加數，2的首次出現位置必然在第1和 $n+1$ 的被加數之間。2在不同位置的情況都考慮到後，得出 $F_{n}+F_{n-1}+...+F_{0}$ 為要求的數目。

$F_{1}+2F_{2}+3F_{3}+...+nF_{n}=nF_{n+2}-F_{n+3}+2$

$F_{1}+F_{3}+F_{5}+...+F_{2n-1}=F_{2n}$
$F_{2}+F_{4}+F_{6}+...+F_{2n}=F_{2n+1}-1$
${F_{1}}^{2}+{F_{2}}^{2}+{F_{3}}^{2}+...+{F_{n}}^{2}=F_{n}F_{n+1}$
$F_{n-1}F_{n+1}-{F_{n}}^{2}=(-1)^{n}$

定理

資料來源：[3]

{\begin{aligned}{F_{m}}{F_{n}}+{F_{m-1}}{F_{n-1}}&=F_{m+n-1}\\F_{m}F_{n+1}+F_{m-1}F_{n}&=F_{m+n}\end{aligned}}

特別地，當m = n時，

{\begin{aligned}F_{2n-1}&=F_{n}^{2}+F_{n-1}^{2}\\F_{2n}&=(F_{n-1}+F_{n+1})F_{n}\\&=(2F_{n-1}+F_{n})F_{n}\end{aligned}}

$F_{n}$ 整除 $F_{m}$ ，若且唯若n整除m，其中n≧3。
$\gcd(F_{m},F_{n})=F_{\gcd(m,n)}$
任意連續三個菲波那契數兩兩互質，亦即，對於每一個n，

gcd(F_n, F_n+1) = gcd(F_n, F_n+2) = gcd(F_n+1, F_n+2) = 1

應用

1970年，尤裏·馬季亞謝維奇指出了偶角標的斐波那契函數

y=F_{2x}

正是滿足Julia Robison假設的丟番圖函數，因而證明了希爾伯特第十問題是不可解的。

程式參考

JavaScript 迭代版

function fib(n) {
    var fib_n = function(curr, next, n) {
        if (n == 0) {
            return curr;
        }
        else {
            return fib_n(next, curr+next, n-1);
        }
    }
    return fib_n(0, 1, n);
}
alert(fib(40));

C语言通项公式版

#include <stdio.h>
#include <math.h>

int main()
{
    int n;
    double constant_a = (1 + sqrt(5)) / 2;
    double constant_b = (1 - sqrt(5)) / 2;
    double constant_c = sqrt(5) / 5;
    double value_1 = 0;
    int value_2 = 0;
    scanf("%d", &n);
    if(n > 0)
    {
        for (int i = 0; i < n; i++)
        {
             value_1 = constant_c * (pow(constant_a, i) - pow(constant_b, i));
             value_2 = (int)value_1;
             printf("%d\n", value_2);
        }
        return 0;
    }
    else
    {
        return -1;
    }
}

c++通项公式版

#include <iostream>
#include <cmath>
using namespace std;
int main()
{
    unsigned long long n;
    double ca = (1 + sqrt(5)) / 2;
    double cb = (1 - sqrt(5)) / 2;
    double cc = sqrt(5) / 5;
    double v1 = 0;
    double v2 = 0;
    cout <<" ";
    cin>>n;
    if(n > 0)
    {
        for (unsigned long long i = 0; i < n; i++)
    {
            v1 = cc * (pow(ca, i) - pow(cb, i));
        v2 = (int)v1;
        cout <<v2<<endl;
    }
    return 0;
    }
    else
    {
        return -1;
    }
        cout <<'/b';
}

Python语言通项公式版

# Fibonacci numbers module

def fib(n):    # write Fibonacci series up to n
    a, b = 0, 1
    while b < n:
        print(b, end=' ')
        a, b = b, a+b
    print()

def fib2(n):   # return Fibonacci series up to n
    result = []
    a, b = 0, 1
    while b < n:
        result.append(b)
        a, b = b, a+b
    return result

fibs = [0, 1]
numZS = int(input('How many Fibonacci numbers do you want? '))
for i in range(numZS-2):
    fibs.append(fibs[-2] + fibs[-1])
print fibs

Common Lisp

(defun fibs (x)
  (cond ((equal x 0) 1)
        ((equal x 1) 1)
        (t (+ (fibs (- x 1))
              (fibs (- x 2))))))

(defun fibs (x)
  (do ((n 0 (+ n 1))
       (i 1 j)
       (j 1 (+ i j)))
      ((equal n x) i)))

Go

遞迴版，時間複雜度為 O(2^n)：

func fibonacci(n int) int {
	if n < 2 {
		return n
	}

	return fibonacci(n-2) + fibonacci(n-1)
}

通用版，時間複雜度為 O(n)：

func fibonacci(n int) int {
	a, b := n%2, 1

	for i := 0; i < n/2; i++ {
		a += b
		b += a
	}

	return a
}

Java语言通项公式版：

public int fibonacci(int n){
    if(n<2){
     return n;
    }else {
      return fibonacci(n-1)+fibonacci(n-2);
    }
}

Java语言快捷版：

public int fibonacci(int n){
    if(n<2){
     return n;
    }else {
      int[] ans = new int[n];
          ans[0] = 1;
          ans[1] = 2;
          for(int i=2;i<n;i++) {
              ans[i]=ans[i-1]+ans[i-2];
          }
          return ans[n-1];
    }
}

C语言陣列版：

#include <stdio.h>
#include <stdlib.h> 
int main()
{   
     int n,s,L;
     printf("輸入長度");
     scanf("%d",&L);
     while(L<0)
     {
     	printf("錯誤"); 
     	return 0;
	 }
     int a[L]; 
     int x=1,y=2;
     a[0]=x;
     a[1]=x;
     a[2]=y;
	 for(n=3;n<L;n++)
	 {  
		 a[n]=a[n-1]+a[n-2];  	
	 }
       for(n=0;n<L;n++)
     {
         printf("%d ",a[n]);
     }
     system("pause");
     return 0;
}

Python Lambda 遞迴版:

fib = lambda n: n if n<2 else fib(n-1) + fib(n-2)

參考文獻

KNUTH, D. E. 1997. The Art of Computer ProgrammingArt of Computer Programming, Volume 1: Fundamental Algorithms, Third Edition. Addison-Wesley. Chapter 1.2.8.
Arakelian, Hrant (2014). Mathematics and History of the Golden Section. Logos, 404 p. ISBN 978-5-98704-663-0, (rus.)
克裏福德A皮科夫.數學之戀.湖南科技出版社.

.
JOHN H. E. COHN. . Bedford College, University of London, London, N.W.1. （原始内容存档于2012-06-30）. Theorem 3. If F_n = x², then n = 0, ±1, 2 or 12.
李晨滔、馮勁敏. (PDF). 桃園縣立大園國際高中.

參見

齊肯多夫定理

外部連結

費波那契數，孫智宏（pdf）
Periods of Fibonacci Sequences Mod m at MathPages
Scientists find clues to the formation of Fibonacci spirals in nature

Fibonacci Sequence，In Our Time (BBC Radio 4)的《In Our Time》節目。(現在聆聽)
Hazewinkel, Michiel (编), , , Springer, 2001, ISBN 978-1-55608-010-4

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] .

[2] JOHN H. E. COHN. . Bedford College, University of London, London, N.W.1. （原始内容存档于2012-06-30）. Theorem 3. If F_n = x², then n = 0, ±1, 2 or 12.

[性質整理-3] 李晨滔、馮勁敏. (PDF). 桃園縣立大園國際高中.

斐波那契数列

源起

表達式

初等代數解法

首先構建等比數列

求出數列{ $a_{n}+\alpha a_{n-1}$ }

求數列{ $b_{n}$ }進而得到{ $a_{n}$ }

線性代數解法

構建一個矩陣方程

求矩陣的特徵值： $\lambda$

特徵向量

分解首向量

用數學歸納法證明

化簡矩陣方程

求A的表達式

數論解法

組合數解法

近似值

用計算機求解

和黃金分割的關係

與平方數的關係

和自然的關係

恆等式

定理

相關的數列

和盧卡斯數列的關係

反費波那西數列

巴都萬數列

佩爾數列

應用

相關猜想

程式參考

參考文獻

參見

外部連結

斐波那契数列

源起

表達式

初等代數解法

首先構建等比數列

求出數列{ a n + α a n − 1 {\displaystyle a_{n}+\alpha a_{n-1}} }

求數列{ b n {\displaystyle b_{n}} }進而得到{ a n {\displaystyle a_{n}} }

線性代數解法

構建一個矩陣方程

求矩陣的特徵值： λ {\displaystyle \lambda }

特徵向量

分解首向量

用數學歸納法證明

化簡矩陣方程

求A的表達式

數論解法

組合數解法

近似值

用計算機求解

和黃金分割的關係

與平方數的關係

和自然的關係

恆等式

定理

相關的數列

和盧卡斯數列的關係

反費波那西數列

巴都萬數列

佩爾數列

應用

相關猜想

程式參考

參考文獻

參見

外部連結

求出數列{ $a_{n}+\alpha a_{n-1}$ }

求數列{ $b_{n}$ }進而得到{ $a_{n}$ }

求矩陣的特徵值： $\lambda$