模算數
模算數(modular arithmetic)是一個整数的算术系統,其中數字超過一定值後(稱為模)後會「捲回」到較小的數值,模算數最早是出現在卡爾·弗里德里希·高斯在1801年出版的《算术研究》一書中。
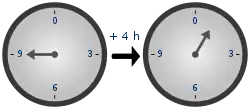
模算數常見的應用是在十二小時制,將一天分為二個以十二小時計算的單位。假設現在七點,八小時後會是三點。用一般的算術加法,會得到7 + 8 = 15,但在十二小時制中,超過十二小時會歸零,不存在「十五點」。類似的情形,若時鐘目前是十二時,二十一小時後會是九點,而不是三十三點。小時數超過十二後會再回到一,為模12的模算數系統。依照上述的定義,12和12本身同餘,也和0同餘,因此12:00的時間也可以稱為是0:00,因為模12時,12和0同餘。
同餘關係
模算數可以在導入整數的同餘關係後,以數學的方式處理,同餘關係和整數的加法、減法及乘法相容。針對正整數n,二個整數a和b對於模n同餘
若二數的差值a − b為n的整數倍數(若n整除a − b)。數字n稱為同餘關係的模。
例如
因為38 − 14 = 24,是12的倍數。
上述的概念也對負數有效:
而a ≡ b mod n也可以用計算带余除法的余数時,a和b除以n的余数相同來表示。例如
因為38和14除以12時,餘數都為2。這是因為38 − 14 = 24是12的整數倍,符合之前同餘關係的定義。
因為常常會考慮不同模數的同餘關係,因此表示同餘關係時會用a ≡ b mod n的表示法。除去三元的表示法不論,同餘關係其實是二元关系,用a ≡n b就可以看出此一特性。
同餘關係可以和加法、減法及乘法一起使用時。若
及
則
若模算數延伸到包括所有实数,上式也成立,也就是說a1, a2, b1, b2, n不一定都是整數,不過以下的關係在不都是整數時可能會不成立:
應用
模算數在数论、群论、环论、紐結理論、抽象代数、電腦代數、密码学、计算机科学及化學中都有使用,也出現在視覺藝術及音乐。
模算數是数论的基礎之一,也提供了群论、环论及抽象代数中一些重要的範例。
模算數也常作為識別碼的校验码。例如国际银行账户号码(IBAN)就用模97的餘數來避免輸入編號時的錯誤。
在密碼學中,模算數是 RSA及迪菲-赫爾曼等公开密钥加密系統的基礎,也提到了和 椭圆曲线有關的有限域,用在許多的系統化鑰演算法中,包括高级加密标准(AES)、國際資料加密演算法(IDEA)、及RC4。RSA和迪菲-赫爾曼密鑰交換用到了模冪。
在電腦代數中,模算數常用來限制中間計算的整數係數大小,也限制計算中用到的資料。模算數用在多項式分解中(其中所有已知有效率的演算法都用到了模算數),而針對整數及有理數的多項式最大公因式、线性代数及Gröbner基,最有效率解法都用到了模算數。
計算機科學中,模算數會以位操作的方式表示,也和其他定長度、循環式的数据结构有關。許多编程语言及计算器中都有模除,而XOR是二個位元在模2下的和。
化學中,表示化合物編號的CAS号,最後一碼是校验码,是將CAS号前二位數乘以1、下一位乘以2,再下一位乘以3……,最後對10取餘數而得。
音樂上,模12的模算數用在十二平均律的系統中,其中有純八度及異名同音的情形(,例如升音符的C音和降音符的D音會視為是同一個音)。
去九法是徒手計算時快速的檢查工具,是以模9的模算數為基礎,而且其中最重要的性質是 10 ≡ 1 (mod 9)。
