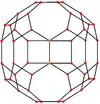
四角化菱形十二面體
在幾何學中,四角化菱形十二面體是一種由48個不等邊三角形組成的卡塔蘭多面體,又稱為六八面體(hexoctahedron)[1][2]、六角化八面體(hexakis octahedron[3][4][5][6])、八角化立方體(octakis cube、octakis hexahedron)、菱形四角化十二面體(kisrhombic dodecahedron[8]),雖然其具有面可遞的性質,然而由於其組成的面不是正多邊形因此不能算是正多面體[9],其對偶多面體為大斜方截半立方體。
| 四角化菱形十二面體 | |
|---|---|
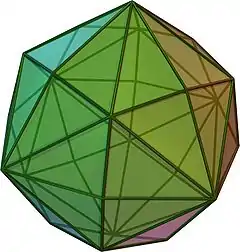 (按這裡觀看旋轉模型) | |
| 類別 | 卡塔蘭立體 |
| 面 | 48 |
| 邊 | 72 |
| 頂點 | 26 |
| 歐拉特徵數 | F=48, E=72, V=26 (χ=2) |
| 面的種類 |  不等邊三角形 |
| 面的佈局 | V4.6.8 |
| 頂點圖 | V4.6.8 |
| 考克斯特符號 | |
| 康威表示法 | mC |
| 對稱群 | Oh, B3, [4,3], *432 |
| 對偶 | 大斜方截半立方体 |
| 旋轉對稱群 | O, [4,3]+, (432) |
| 二面角 | 155° 4' 56" |
| 特性 | 凸、 面可遞 |
 |
 V4.6.8 (頂點圖) |
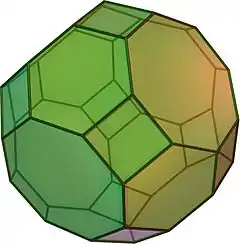 大斜方截半立方体 (對偶多面體) |
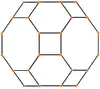
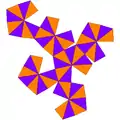 (展開圖) |
性質
四角化菱形十二面體是卡塔蘭立體的一種[10],即阿基米德立體的對偶多面體[11],其對應的阿基米德立體為大斜方截半立方體[12][13]。並具有面可遞的性質,這意味著,這立體上的任意兩個面A和B,透過旋轉或鏡射這個立體,使A移動到B原來的位置時,其面仍然佔據了相同的空間區域[14]。所有的正多面體都擁有這個特性,然而四角化菱形十二面體並未所有邊等長、組成的面也非正多邊形,因此不屬於正多面體[9]。
組成
四角化菱形十二面體共由48個面、72個邊、26個頂點組成,其中48個面為全等的三角形、72條邊則有3種長度,每個長度各24條、26個頂點當中,有12個四面角頂點、8個六面角頂點、和 6個八面角頂點[15]。
四角化菱形十二面體可以將菱形十二面體透過四角化變換來完成,其等價於將菱形十二面體每個面替換成一個頂點和四個三角形[9]或在菱形十二面體的每個面上疊上一個菱形錐來組成四角化菱形十二面體。
對稱性
四角化菱形十二面體具有Oh, B3, [4,3] (*432)的八面體群對稱性。其每條稜皆代表八面體群對稱性的鏡射線。其結構也可以透過將立方體在每個正方形面上以正方形的頂點、邊中點和幾何中心為基準將正方形分成8個三角形、或透過將正八面體在每個三角形面上以正三角形的頂點、邊中點和幾何中心為基準將正三角形分成6個三角形、或透過將菱形十二面體在每個菱形面上以菱形的幾何中心為基準將菱形分成四個三角形來看出。[17]
 四角化菱形十二面體 |
 球面鑲嵌 |
 立方體 |
 正八面體 |
 菱形十二面體 |
球極投影
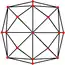
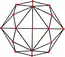
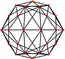
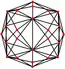
與四角化菱形十二面體對應的球面鑲嵌可透過透過9個球面大圓來構建[18](即四角化菱形十二面體投影到球面的結果)[10],因此在球極平面投影中,四角化菱形十二面體的稜可以在平面上形成9個圓或中心徑向線。這9個圓或中心徑向線可以分成兩組,其中一組由3個圓或中心徑向線組成(下圖以紫色表示)、另一組由6個圓或中心徑向線組成(下圖以紅色表示),分別代表其兩個正交子群,分別是[2,2]和[3,3]:
| 平行投影 | 球極平面投影 | |||
|---|---|---|---|---|
| 圖像 | 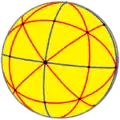 |
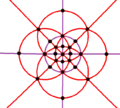 |
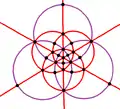 |
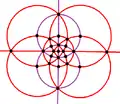 |
| 投影對稱性 | [4] | [3] | [2] | |
相關多面體與鑲嵌
 |
 |
| 領結立方體和領結八面體的對偶多面體是一個外觀與四角化菱形十二面體類似的多面體,其包含了額外的三角形對。[23] | |
四角化菱形十二面體可以將菱形十二面體透過四角化變換來完成,其等價於將菱形十二面體每個面替換成一個頂點和四個三角形[9],而菱形十二面體可以經由立方體透過會合變換構造,即將立方體每個面貼上角錐,並用適當的錐高,使角錐側面與鄰近面上貼的角錐之測面共面來獲得。亦可以從其對偶多面體大斜方截半立方体經對偶變換而來,而四角化菱形十二面體也可以變換回其對偶大斜方截半立方体[24],而大斜方截半立方体也是立方体經過康威變換的結果。因此四角化菱形十二面體可以視為一個以立方體為出發點經由2次康威變換來完成。其他也是由立方體為出發點經由有限次的康威變換產生的多面體有:
| 对称性: [4,3], (*432) | [4,3]+, (432) | [1+,4,3], (*332) | [4,3+], (3*2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
||||||
| {4,3} | t0,1{4,3} | t1{4,3} | t1,2{4,3} | {3,4} | t0,2{4,3} | t0,1,2{4,3} | s{4,3} | h{4,3} | h1,2{4,3} |
| 半正多面体的对偶 | |||||||||
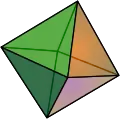 |
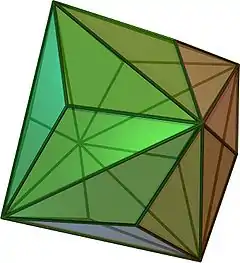 |
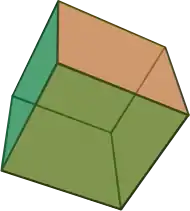 |
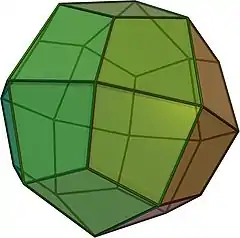 |
 |
 | ||||
| V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
 |
 |
 |
 |
| 菱形十二面體 | 四角化菱形十二面體 | 星形四角化菱形十二面體 | 反平行四邊形二十四面體 |
在面的布局中,四角化菱形十二面體可以寫成V4.6.8 ,其意義為其面由3個頂點組成,每個頂點依序是:四個面的公共頂點、六個面的公共頂點和八個面的公共頂點[25]。其可以進一步的列在V4.6.2n的無窮序列中n為4的位置。
| *n32變異對稱性4.6.2n的全截鑲嵌系列: | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 對稱性 *n32 [n,3] |
球面鑲嵌 | 歐氏鑲嵌 | 緊湊雙曲 | 仿緊雙曲 | 非緊雙曲 | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| 圖像 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| 頂點 | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| 對偶 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 面 | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
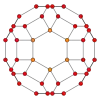
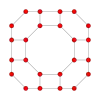
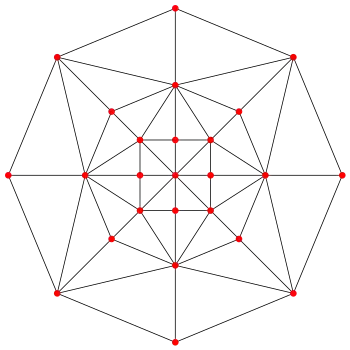
四角化菱形十二面體圖
| 四角化菱形十二面體圖 | |
|---|---|
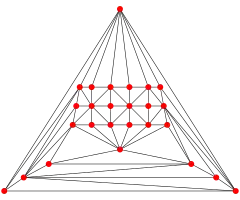 | |
| 度分布 | 4 (12個) 6 (8個) 8 (6個) |
| 顶点 | 26 |
| 边 | 72 |
| 半径 | 4[26] |
| 直径 | 4[26] |
| 围长 | 3 |
| 色数 | 3[26] |
| 對偶圖 | 大斜方截半立方體圖 |
| 属性 | 平面, 可積 |
在圖論的數學領域中,與四角化菱形十二面體相關的圖為四角化菱形十二面體圖(Disdyakis Dodecahedral Graph),是四角化菱形十二面體之邊與頂點的圖[26],是一個阿基米德對偶圖[27]。
參考文獻
- Williams, Robert. . Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- . Florida Center for Instructional Technology, College of Education, University of South Florida. [2019-09-02]. (原始内容存档于2018-08-28).
- . 國家教育研究院. [2019-09-01]. (原始内容存档于2019-09-02).
- Unkelbach, H. 5. Deutsche Math. 1940: pp. 306-316.
- Holden, A. . Dover Publications. 1971: p. 55.
- . 3dwarehouse.sketchup.com.
- Eric W. Weisstein. . 密西根州立大學. 1999-05-26 [2019-09-01]. (原始内容存档于2013-06-21).
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 285, kisRhombic dodecahedron)
- Conway, Symmetries of things[7], p.284
- . Florida Center for Instructional Technology, College of Education, University of South Florida. [2019-09-03]. (原始内容存档于2015-01-21).
- Ambroszkiewicz, Stanislaw and Baranski, Miroslaw. . arXiv preprint arXiv:1904.05173. 2019: pp. 30-34.
- Gurkewitz, R. and Arnstein, B. . Dover Origami Papercraft. Dover Publications. 2012: p. 31. ISBN 9780486136776.
- Eric W. Weisstein. . 密西根州立大學. 1999-05-26 [2019-09-01]. (原始内容存档于2013-06-04).
- Keinan, E. and Schechter, I. . Wiley. 2001: p. 146. ISBN 9783527302352. LCCN 2001272200.
- McLean, K. Robin, , The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822.
- David I. McCooey. . dmccooey.com. 2015 [2019-09-02]. (原始内容存档于2019-09-02).
- 埃里克·韦斯坦因. . MathWorld.
- . [2019-09-02]. (原始内容存档于2019-02-13).
- Huylebrouck, Dirk. . The Mathematical Intelligencer (Springer). 2018, 40 (1): 18––23.
- 約翰·史坦布里奇. . math.lsa.umich.edu. [2019-09-05]. (原始内容存档于2018-02-10).
- 約翰·史坦布里奇. . math.lsa.umich.edu. [2019-09-05]. (原始内容存档于2017-08-21).
- 金原博昭. (PDF). orion-metaphysics.com. 2010年6月1日 (日语).
- . fillygons.ch. [2019-09-03]. (原始内容存档于2019-09-08).
- Kaplan, Craig S and Hart, George W; 等, , Waterloo Computer Graphics Lab, [2019-09-02], (原始内容存档于2017-03-17)
- Verbiese, Samuel; 等, (PDF), Proceedings of the Bridges Conference in London, 2006 [2019-09-04], (原始内容存档 (PDF)于2017-08-09)
- Walter Steurer, Deloudi Sofia. 126. Springer Science, Business Media. 2009: pp. 18–20, 51–53 [2019-09-03]. (原始内容存档于2017-02-02).
- 埃里克·韦斯坦因. . MathWorld.
- 埃里克·韦斯坦因. . MathWorld.
外部連結
- 埃里克·韦斯坦因, 四角化菱形十二面體 (參閱Catalan solid) 於MathWorld(英文)
- Disdyakis Dodecahedron (Hexakis Octahedron) Interactive Polyhedron Model