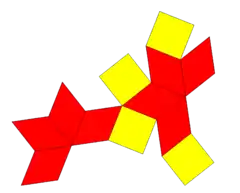
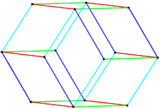
菱形十二面體
在幾何學中,菱形十二面體()是一個由菱形構成的十二面體[2],屬於卡塔蘭立體,由12個全等的菱形組成,具有24條邊和14個頂點,其對偶多面體為截半立方體[3]。
| 菱形十二面體 | |
|---|---|
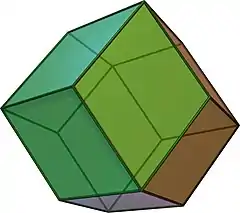 (點選檢視旋轉模型) | |
| 類別 | 卡塔蘭立體 |
| 面 | 12 |
| 邊 | 24 |
| 頂點 | 14 |
| 歐拉特徵數 | F=12, E=24, V=14 (χ=2) |
| 面的佈局 | V3.4.3.4 菱形 |
| 頂點佈局 | 8{3}+6{4} |
| 考克斯特符號 | |
| 康威表示法 | jC |
| 對稱群 | Oh, B3, [4,3], (*432) |
| 對偶 | 變數 "對偶多面體" 未定義。 |
| 旋轉對稱群 | O, [4,3]+, (432) |
| 二面角 | 120°[1]:5 |
| 特性 | 凸、面可遞、等面、等邊、平行體 |
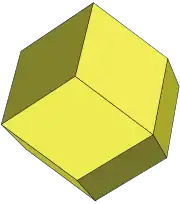 | |
 變數 "對偶多面體" 未定義。 (對偶多面體) |
 (展開圖) |

性質
菱形十二面體是一個卡塔蘭立體,由12個面、24條邊和14個頂點[1]:3,其中12面為12個全等的個菱形,且具有180度旋轉對稱性和點對稱性,因此是一個環帶多面體[4],其對偶多面體為截半立方體。
菱形十二面體能獨立密鋪三維空間,因此是一種空間填充多面體[5],其所形成的堆砌體可以視為是面心立方晶格的沃罗诺伊鑲嵌。這種堆砌體是體心立方晶格(bcc)的布里元區,部分礦物可以形成於菱形十二面體的晶體慣態[6],如石榴石。蜜蜂築巢時也是使用菱形十二面體空間填充的幾何結構來築巢,其每個蜂房皆是以半個菱形十二面體為上蓋之六角柱的空間填充構成[7][8]。菱形十二面體也出現在鑽石和金剛石的單位晶格中,但實際上少了4個頂點,而化學鍵位於剩餘的稜上[9]。
菱形十二面體可以從中心分割成4個三方偏方面體,若將菱形十二面體空間填充的每一個菱形十二面體都分割成三方偏方面體則可以形成三方偏方面體的空間填充[10][11],這意味著三方偏方面體也可以獨立密鋪三維空間。這種切割就好像將正六邊形鑲嵌的六邊形切割成3個菱形而形成菱形鑲嵌。
對稱性
菱形十二面體的對偶多面體——截半立方體是一個阿基米德立體,具有點可遞的性質,因此菱形十二面體具有面可遞的性質,這意味著這個幾何形狀的對稱群可在各個面上傳遞,換句話說,這立體上的任意兩個面A和B,若透過旋轉或鏡射這個立體,使A移動到B原來的位置時,而兩個面仍然佔據了相同的空間區域[13]。
同理,菱形十二面體具有邊可遞的特性,這意味著,這立體上的任意兩條稜A和B,透過旋轉或鏡射這個立體,使A移動到B原來的位置時,其稜以及其二面角仍然佔據了相同的空間區域[14][15][16]。菱形十二面體是9個邊可遞的凸多面體之一,其他8個分別是五個柏拉圖立體、截半立方體、截半二十面体和菱形三十面體。
正交投影
菱形十二面體有4個特殊的正交投影,分別為於四個菱形的公共頂點投影、於三個菱形的公共頂點投影、於稜上投影和於面上投影,其中「於稜上投影」以及「於面上投影」其對稱性對應於B2 和 A2的考克斯特平面[21]。
| 投影 對稱性 |
[4] | [6] | [2] | [2] |
|---|---|---|---|---|
| 菱形 十二面體 |
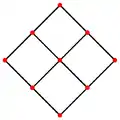 |
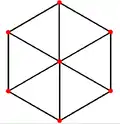 |
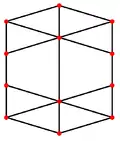 |
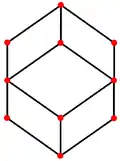 |
| 截半立方體 (對偶) |
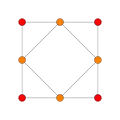 |
 |
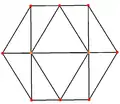 |
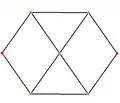 |
其他菱形十二面體
亦有一些十二面體也是由菱形組成,例如比林斯基十二面體。
平行十二面體
菱形十二面體是一種平行多面體,具有可以獨立填滿三維空間填充,所形成的幾何結構稱為菱形十二面體堆砌或平行十二面體堆砌,其對偶可能為半立方體堆砌或由四面體和八面體組成的堆砌。
 由菱形十二面體堆砌而成的幾何結構 |
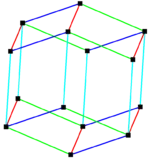 平行十二面體可由四對等長的邊組成。 |
常見的由菱形組成的平行十二面體有二面體群菱形十二面體。
相關多面體與鑲嵌
菱形十二面體可以經由立方體透過會合變換構造,即將立方體每個面貼上角錐,並用適當的錐高,使角錐側面與鄰近面上貼的角錐之測面共面來獲得。其他也是由立方體透過康威變換得到的多面體有:
| 对称性: [4,3], (*432) | [4,3]+, (432) | [1+,4,3], (*332) | [4,3+], (3*2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
||||||
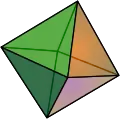
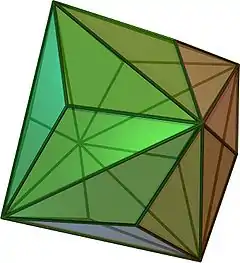
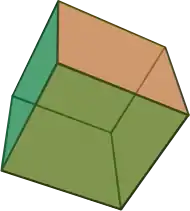
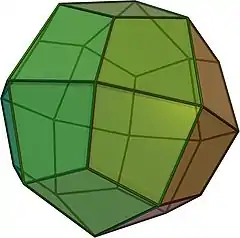
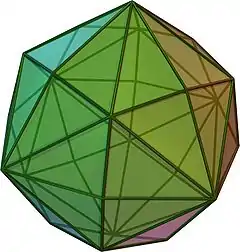
| {4,3} | t0,1{4,3} | t1{4,3} | t1,2{4,3} | {3,4} | t0,2{4,3} | t0,1,2{4,3} | s{4,3} | h{4,3} | h1,2{4,3} |
| 半正多面体的对偶 | |||||||||
 |
 |
 |
 |
 |
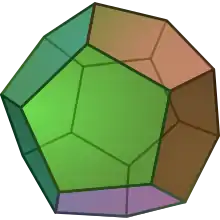 | ||||
| V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
菱形十二面體可以切割成截半立方體。在切割過程可以得到一些不同的多面體,例如:
| (可能的來源) | 倒角立方體 (截邊立方體) |
截角倒角立方體 (截邊截角立方體) |
截半倒角立方體 (截邊截半立方體) |
截半立方體 | |
|---|---|---|---|---|---|
| 圖像 |  菱形十二面體 |
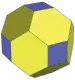 倒角立方體 |
 小斜方截半立方体 |
 大斜方截半立方体 |
 截半立方體 |
| 考克斯特符號 | |||||
| 對偶多面體 | |||||
| 對偶 |  截半立方體 |
 四角化截半立方體 |
 鳶形二十四面體 |
 六角化八面體 |
 菱形十二面體 |
| 考克斯特符號 | |||||
菱形十二面體與小斜方截半四面體(等價於截半立方體)的對偶多面體等價,其他與正四面體相關的多面體為:
| 对称性: [3,3], (*332) | [3,3]+, (332) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 | |||
| {3,3} | t0,1{3,3} | t1{3,3} | t1,2{3,3} | t2{3,3} | t0,2{3,3} | t0,1,2{3,3} | s{3,3} |
| 半正多面体对偶 | |||||||
 |
 |
 |
 | ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
菱形十二面體可以視為由菱形組成的球面鑲嵌圖,一般菱形鑲嵌的菱形銳角頂點是3個菱形的公共頂點,有這種性質的相關多面體與鑲嵌包括:
| 擬正鑲嵌對稱性 3.4.n.4: V(3.n)2 的變種: | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| *n32 | 球面鑲嵌 | 歐氏鑲嵌 | 緊湊鑲嵌 | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| 鑲嵌圖 |  |
 |
 |
 |
 |
 |
 | ||||
| 布局 | V(3.3)2 | V(3.4)2 | V(3.5)2 | V(3.6)2 | V(3.7)2 | V(3.8)2 | V(3.∞)2 | ||||
另一種菱形鑲嵌的菱形銳角頂點是4個菱形的公共頂點,而菱形十二面體也屬於這類鑲嵌。有這種性質的相關多面體與鑲嵌包括:
| *n42 擬正對偶鑲嵌對稱性 V(4.n)2 的變種: | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 對稱性 *4n2 [n,4] |
球面鑲嵌 | 歐氏鑲嵌 | 緊湊鑲嵌 | 仿緊鑲嵌 | 非緊鑲嵌 | ||||||
| *342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] |
[iπ/λ,4] | ||||
| 鑲嵌圖 布局 |
 V4.3.4.3 |
 V4.4.4.4 |
 V4.5.4.5 |
 V4.6.4.6 |
 V4.7.4.7 |
 V4.8.4.8 |
 V4.∞.4.∞ |
V4.∞.4.∞ | |||
此外,菱形十二面體也可以對應到面布局為V3.2n.3.2n的鑲嵌圖系列中。這個系列的第一種形狀時平面鑲嵌,其餘皆為雙曲鑲嵌:
 V3.4.3.4 (展開圖) |
 V3.6.3.6 平面鑲嵌 菱形鑲嵌 |
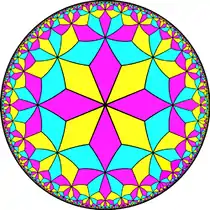 V3.8.3.8 雙曲鑲嵌 (龐加萊圓盤模型) |
拓樸同構的多面體
部分多面體與菱形十二面體拓樸同構,例如平行十二面體,亦有一些非菱形組成的十二面體與菱形十二面體拓樸同構,例如鳶形十二面體。
鳶形十二面體

鳶形十二面體[28][29][30]是一種由24個全等的鳶形組成的十二面體,具有面可遞的性質,並具24階四面體群對稱性。
鳶形十二面體可以視為將菱形十二面體的菱形面變形成鳶形的結果。形變的方式是透過調整菱形十二面體的8個頂點,另外四個頂點保持正四面體的布局位置。其形變量可透過一個數組(a,b)來表示,當a和b皆為1時則為菱形十二面體,a表示保持著正四面體的布局位置的頂點,可以逐漸向12趨近,向12趨近的意義表示其頂點逐漸移向幾何中心;而b的值取決於a,需要使移動時能夠成平面的鳶形而非扭歪多邊形,其值會向正無窮大逼近。這種情形下,其頂點坐標可以表示為:
- (±2, 0, 0), (0, ±2, 0), (0, 0, ±2)
- (a, a, a), (−a, −a, a), (−a, a, −a), (a, −a, −a)
- (−b, −b, −b), (−b, b, b), (b, −b, b), (b, b, −b)
下表列出部分數組(a,b)所形成的鳶形十二面體圖像:
| 數組(a,b) | (1,1) | (78,76) | (34,32) | (23,2) | (58,52) | (916,92) |
|---|---|---|---|---|---|---|
| 圖像 |  |
 |
 |
 |
 |
 |
星形化體

如同其他的凸多面體,菱形十二面體也可以透過延伸面或邊,直到它們相遇形成新的多面體來進行星形化。多爾曼·露可(Dorman Luke)在他的論文中描述了一些菱形十二面體的星形化體[31]。較廣為人知的是他提出的第一種多面體,其名稱可以簡略地稱為「第一種星形菱形十二面體」。這種多面體可以視為將適當錐高的菱形錐(底面為菱形的四角錐)疊在菱形十二面體的每一個菱形面上,並且讓錐高高於鄰近的面來構造:
 第一種星形菱形十二面體
第一種星形菱形十二面體 第一種星形菱形十二面體的三維模型
第一種星形菱形十二面體的三維模型
對偶複合體
對偶複合體是由一個多面體與其對偶多面體組合成的複合圖形。菱形十二面體與其對偶的複合體為複合截半立方體菱形十二面體。其共有26個面、48條邊和26個頂點,其尤拉示性數為4,虧格為-1[32]。
截角菱形十二面體
截去所有頂點後的菱形十二面體稱為截角菱形十二面體。
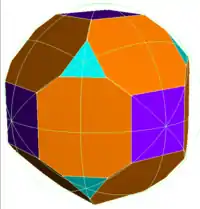 |
| 截角菱形十二面体 |
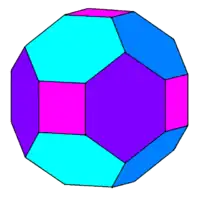
若将菱形十二面体的六个发出四条棱的顶点截去可以獲得倒角立方體[33]。
 |
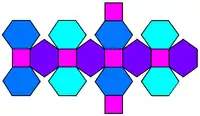 |
| 倒角立方體 | 倒角立方體的展开图 |
另外若将菱形十二面体的八个发出三条棱的顶点截去可以獲得倒角八面體[4][34]。
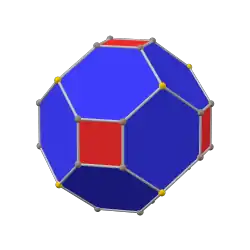 倒角立方體 |
 菱形十二面體 |
 倒角八面體 |
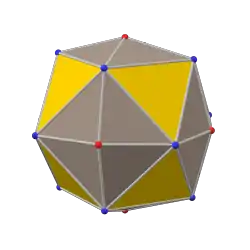 四角化截半立方體 |
 截半立方體 |
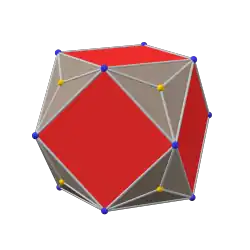 三角化截半立方體 |
菱形十二面體堆砌
菱形十二面體可以獨立填滿三維空間,其所形成的幾何結構稱為菱形十二面體堆砌。
參考文獻
- Cromwell, P. . United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
- Robert W. Gray. (PDF). rwgrayprojects.com. September 5, 2007 [2018-08-29]. (原始内容存档 (PDF)于2015-07-09).
- 埃里克·韦斯坦因. . MathWorld.
- 埃里克·韦斯坦因. . MathWorld.
- George W. Hart. . The Mathematica Journal. 1999, vol. 7 (no. 3) [2018-08-29]. (原始内容存档于2018-11-14).
- Eric W. Weisstein. . 1999-05-25 [2018-08-29]. (原始内容存档于2013-06-03).
- Stewart, Ian. . Weidenfeld & Nicolson. 2001. pp. 82-84
- Nazzi, F. . Scientific Reports. 2016, 6: 28341. PMC 4913256. PMID 27320492. doi:10.1038/srep28341.
- . calfss.edu.hk. [2018-08-29]. (原始内容存档于2018-08-29).
- Dodecahedral Crystal Habit 的存檔,存档日期2009-04-12.. khulsey.com
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
- 李政憲、翁條雄、連崇馨. . 科學研習. 2017年5月, (No.56-05): 24-32 [2018-08-29]. (原始内容存档于2018-08-29).
- McLean, K. Robin, , The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822.
- Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN 0-521-55432-2, p. 371 Transitivity
- Grünbaum, Branko; and Shephard, G. C. . New York: W. H. Freeman. 1987. ISBN 0-7167-1193-1. (6.4 Isotoxal tilings, 309-321)
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P., , Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1954, 246: 401–450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003
- Weisstein, E.W. . CRC Press. 2002: 2456-2457. ISBN 9781420035223.
- 約翰.布雷克伍德(John Blackwood). . 商周出版. 2018: 42. ISBN 9789864774944.
- . dmccooey.com. [2018-08-26]. (原始内容存档于2018-04-13).
- . 國家教育研究院. [2018-08-27]. (原始内容存档于2018-08-26).
- Coxeter Planes 页面存档备份,存于 and More Coxeter Planes 页面存档备份,存于 約翰·史坦布里奇
- Order in Space: A design source book, Keith Critchlow, p.56–57
- 宮崎興二・山口哲・石井源久『高次元図形サイエンス 页面存档备份,存于』京都大学学術出版会
- P.R. クロムウェル『 多面体』シュプリンガー・フェアラーク東京
- Branko Grünbaum. (PDF) 32 (4): 5–15. 2010. (原始内容 (PDF)存档于2015-04-02).
- H.S.M Coxeter, "Regular polytopes", Dover publications, 1973.
- 郭君逸. . davidguo.idv.tw. 2018-01-23 [2018-08-29]. (原始内容存档于2016-10-04).
- Crook, T. . Longmans, Green and Company. 1921: p.8. LCCN 21002127.
- 埃里克·韦斯坦因. . MathWorld.
- . loki3.com. [2018-09-04]. (原始内容存档于2018-09-01).
- Luke, D. . The Mathematical Gazette. 1957, 337: 189–194.
- . bulatov.org. [2018-09-04]. (原始内容存档于2017-12-06).
- . . geocities.jp. 2005-04-13 [2018-08-29]. (原始内容存档于2018-10-08) (日语).
- a truncated form of the rhombic dodecahedron 页面存档备份,存于 robertlovespi.net 2014-6-9 [2016-1-17]
- 埃里克·韦斯坦因. . MathWorld.
延伸閱讀
- Williams, Robert. . Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus. . Cambridge University Press. 1983. ISBN 978-0-521-54325-5. MR 730208. doi:10.1017/CBO9780511569371. (The thirteen semiregular convex polyhedra and their duals, Page 19, Rhombic dodecahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, p. 285, Rhombic dodecahedron )
外部連結
- 埃里克·韦斯坦因, 菱形十二面體 (參閱卡塔蘭立體) 於MathWorld(英文)
- Virtual Reality Polyhedra – The Encyclopedia of Polyhedra
- 電腦模型
- Relating a Rhombic Triacontahedron and a Rhombic Dodecahedron, Rhombic Dodecahedron 5-Compound and Rhombic Dodecahedron 5-Compound by Sándor Kabai, Wolfram 演示项目.
- Rhombic Dodecahedron Calendar:不須使用膠水製作一個菱形十二面體月曆
- Another Rhombic Dodecahedron Calendar:由編織紙條製成的菱形十二面體
- 實際應用
- Archimede Institute 使用此菱形十二面體的實際住房建設項目的示例