气体
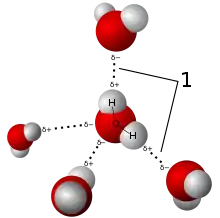
气体(英語:gas,舊稱瓦斯)是四种基本物质状态之一(其他三种分别为固体、液体、等离子体)。气体可以由单个原子(如稀有气体)、一种元素组成的单质分子(如氧气)、多种元素组成化合物分子(如二氧化碳)等组成。气体混合物可以包括多种气体物质,比如空气。气体与液体和固体的显著区别就是气体粒子之间间隔很大。这种间隔使得人眼很难察觉到无色气体。气体与液体一样是流体:它可以流动,可变形、壓縮。假如没有限制(容器或力场)的话,气体可以扩散,其体积不受限制,沒有固定。气态物质的原子或分子相互之间可以自由运动。

氣體的特性介於液體和等离子体之間,氣體的溫度不會超過等离子体,氣體的溫度下限為簡併態夸克氣體[1],現在也越來越受到重視[2]。高密度的原子氣體冷卻到非常低的低溫,可以依其統計特性分為玻色氣體和費米氣體,其他相態可以參照相態列表。
元素氣體
在標準狀況下為氣體分子的化學元素有氫(H2)、氮 (N2)、氧(O2)和兩種鹵素,分別是氟(F2)和氯(Cl2)。另外還有單原子的稀有气体:氦(He)、氖(Ne)、氬(Ar)、氪(Kr)、氙(Xe)和氡(Rn)。
物理性质

因为大多数气体很难直接观察,他们常被通过其四个物理属性或宏观性质来描述:压强、体积、粒子数目(化学家用摩尔来表示)和温度。这四个属性被许多科学家(如罗伯特·波义耳、雅克·查理、约翰·道尔顿、约瑟夫·路易·盖-吕萨克、阿莫迪欧·阿伏伽德罗等)通过不同的气体和不同的裝置来反复观察过。他们的仔细研究最终形成了描述这些属性的数学关系的理想气体定律。
宏观属性
当观察气体时,一般会指明参考物或长度尺度。较大的长度尺度对应着气体的宏观属性或是总体看法。其范围(可指体积)至少要能容纳大量的气体粒子。对如此采样尺寸的气体的统计分析会得到样品内所有气体粒子的平均属性(例如速度,温度,压强等)。相反,一个较小的参考长度尺度对应着气体的微观属性或是粒子层面的看法。
壓力
在公式中常用"p"或"P"来表示气体壓力,其单位则常为国际单位制中的帕斯卡(Pa)。
在描述一個有容器的氣體時,壓力(或是絕對壓力)是在氣體作用在容器上,單位面積所施的力,在此空間內,可以視為氣體粒子會直線運動,直到和其他分子或是容器壁碰撞為止。若和容器壁碰撞,單位時間內氣體粒子動量的變化就是氣體作用在容器上的力[3],在碰撞過程中,只有垂直容器壁的氣體粒子速度分量會變化,若氣體粒子是沿著容器壁運動,其動量不會變化。因此容器壁受到的力就是和容器壁碰撞的氣體粒子其動量變化的平均值。
壓強是所有碰撞容器壁的氣體粒子,其產生的力除以容器壁總面積後的值。
温度
在公式中常用"T"来表示气体温度,其单位则常为国际单位制中的开尔文(K)。
氣體粒子的速度和其絕對溫度成正比。在右邊的影片中,當氣球放進液態氮中時,因為溫度降低,氣體粒子速度變慢,氣球體積也隨之縮小。氣體系統的溫度和其中粒子(原子或分子)的運動有關[4]。在統計力學中,溫度可以表示儲存在粒子中的平均動能。儲存能量的方式和粒子的自由度有關。藉由氣體粒子碰撞,粒子產生平移、旋轉或是振動的運動,其動能也隨之提高。相反的,固體中的分子因為在晶格中,無法有平移或旋轉的運動,只能以振動的方式提高溫度。加熱的氣體,因為持續和容器或其他氣體粒子碰撞,其速度分佈範圍較大,可以用麦克斯韦-玻尔兹曼分布描述,此時會假設氣體粒子近似為接近熱力學平衡狀態下的理想氣體。
微观属性
分子运动论
分子运动论通过考虑气体颗粒的成分和运动来对气体的宏观属性提供一个内在的视角。
布朗运动
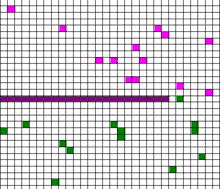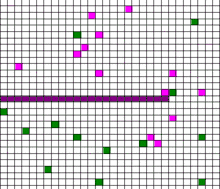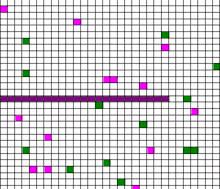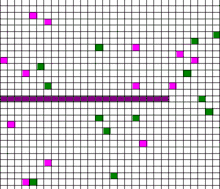
布朗运动是描述流體中粒子隨機運動的數學模型。右圖動畫中粉紅色和綠色的粒子說明氣體運動的方式。
模型
历史成果
特殊主題
可壓縮性

熱力學家利用可壓縮係數(Z)來調整理想氣體方程式,考慮真實氣體可壓縮性的影響。可壓縮係數是實際比容和理想比容之間的比例。一般而言其數值很接近1,可壓縮係數圖描述可壓縮係數和溫度之間的變化。
雷諾數
在流體機械上,雷諾數是慣性力(vsρ)和粘滯力(μ/L)之間的比例,是流體力學中最重要的無因次量,常和其他無因次量配合使用來提供動態相似性的準則。雷諾數可以提供模型和全尺寸的實際條件之間的相關性,也常用來作為流體的分類。
黏度
黏度是有關相鄰粒子之間影響程度的物理量。固體因為內部的分子間作用力,可以承受剪力,流體在類似的剪力下則會持續的變形,氣體的黏度比液體小,不過仍可以觀測到黏度的影響,若是氣體沒有黏度,就不會黏在機翼的表面形成邊界層。一個有關三角翼紋影照相的研究可以看出氣體分子之間會粘在一起(參照「邊界層」一節)。
紊流

紊流是指流場有隨機的、混沌的變化,包括少量的動量擴散,大量的動量對流,壓強和速度在空間和時間上有快速的變化。
邊界層
當氣體粒子沿著一物體表面流過時,有些粒子會因物體表面而速度變慢,好像粘在物體表面一樣,這稱為邊界層。主要是因為表面的摩擦力造成。物體和上面的邊界層會影響後面的流體,而邊界層也會和物體表面分離,形成新的表面,並且改變流體流動的路徑。像飛機的失速就是因為邊界層分離使得機翼的升力下降。
熱力學平衡
當系統中沒有能量轉移時,此系統已達到熱力學平衡。一般而言此時系統和週圍的溫度相同,因此不會有熱的轉移。這也表示外力是平衡的,系統體積不會變化,系統中的化學反應也已完成。熱力學平衡需要的時間隨系統而不同,像冰塊在室溫下約花幾個小時才能融化,在半導體內,一元件由開到關產生的熱轉移可能只需要數奈秒的時間。
参见
参考文献
| 维基共享资源中相关的多媒体资源:气体 |
- T. Zelevinski的工作和有關鍶元素和此領域相關的研究有關,參見Tanya Zelevinsky. . Physics. 2009, 2: 94 [2014-08-05]. Bibcode:2009PhyOJ...2...94Z. doi:10.1103/physics.2.94. (原始内容存档于2014-10-30).
- Quantum Gas Microscope Offers Glimpse Of Quirky Ultracold Atoms 页面存档备份,存于. ScienceDaily. 4 November 2009.
- J. Clerk Maxwell. . Mineola: Dover Publications. 1904: 319–20. ISBN 0-486-41735-2.
- pages 137–8 of Society, Cornell (1907)
- Kenneth Wark. 3. McGraw-Hill. 1977: 12. ISBN 0-07-068280-1.
- Halliday, David; Resnick, Robert; Walker, Jerl, 7th, USA: John Wiley and Sons, Inc., 2005, ISBN 0-471-23231-9
- . 國科會高瞻自然科學教學資源平台. [2014-08-06]. (原始内容存档于2014-08-08).
- . 國家教育研究院. [2014-08-06]. (原始内容存档于2016-03-05).
- . Web.kmsh.tnc.edu.tw. [2014-08-06]. (原始内容存档于2016-03-04).
- . Content.edu.tw. [2014-08-06]. (原始内容存档于2014-07-17).
- . 國科會高瞻自然科學教學資源平台. [2014-08-06]. (原始内容存档于2015-09-10).