K-近邻算法
在模式识别领域中,最近鄰居法(KNN算法,又譯K-近邻算法)是一种用于分类和回归的無母數統計方法[1]。在这两种情况下,输入包含特徵空間(Feature Space)中的k个最接近的训练样本。
- 在k-NN分类中,输出是一个分类族群。一个对象的分类是由其邻居的“多数表决”确定的,k个最近邻居(k为正整数,通常较小)中最常见的分类决定了赋予该对象的类别。若k = 1,则该对象的类别直接由最近的一个节点赋予。
- 在k-NN回归中,输出是该对象的属性值。该值是其k个最近邻居的值的平均值。
| 机器学习与資料探勘 |
|---|
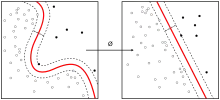 |
最近鄰居法採用向量空間模型來分類,概念為相同類別的案例,彼此的相似度高,而可以藉由計算與已知類別案例之相似度,來評估未知類別案例可能的分類。
K-NN是一种基于实例的学习,或者是局部近似和将所有计算推迟到分类之后的惰性学习。k-近邻算法是所有的机器学习算法中最简单的之一。
无论是分类还是回归,衡量邻居的权重都非常有用,使较近邻居的权重比较远邻居的权重大。例如,一种常见的加权方案是给每个邻居权重赋值为1/ d,其中d是到邻居的距离。[註 1]
邻居都取自一组已经正确分类(在回归的情况下,指属性值正确)的对象。虽然没要求明确的训练步骤,但这也可以当作是此算法的一个训练样本集。
k-近邻算法的缺点是对数据的局部结构非常敏感。
K-平均算法也是流行的机器学习技术,其名稱和k-近邻算法相近,但兩者没有关系。数据标准化可以大大提高该算法的准确性[2][3]。
算法
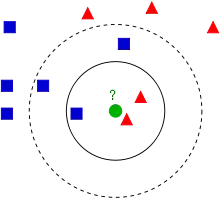
训练样本是多维特征空间向量,其中每个训练样本带有一个类别标签。算法的训练阶段只包含存储的特征向量和训练样本的标签。
在分类阶段,k是一个用户定义的常数。一个没有类别标签的向量(查询或测试点)将被归类为最接近该点的k个样本点中最频繁使用的一类。
一般情况下,将欧氏距离作为距离度量,但是这是只适用于连续变量。在文本分类这种离散变量情况下,另一个度量——重叠度量(或海明距离)可以用来作为度量。例如对于基因表达微阵列数据,k-NN也与Pearson和Spearman相关系数结合起来使用。[4]通常情况下,如果运用一些特殊的算法来计算度量的话,k近邻分类精度可显著提高,如运用大间隔最近邻居或者邻里成分分析法。
“多数表决”分类会在类别分布偏斜时出现缺陷。也就是说,出现频率较多的样本将会主导测试点的预测结果,因为他们比较大可能出现在测试点的K邻域而测试点的属性又是通过k邻域内的样本计算出来的。[5]解决这个缺点的方法之一是在进行分类时将样本到k个近邻点的距离考虑进去。k近邻点中每一个的分类(对于回归问题来说,是数值)都乘以与测试点之间距离的成反比的权重。另一种克服偏斜的方式是通过数据表示形式的抽象。例如,在自组织映射(SOM)中,每个节点是相似的点的一个集群的代表(中心),而与它们在原始训练数据的密度无关。K-NN可以应用到SOM中。
参数选择
如何选择一个最佳的K值取决于数据。一般情况下,在分类时较大的K值能够减小噪声的影响,[6] 但会使类别之间的界限变得模糊。一个较好的K值能通过各种启发式技术(见超参数优化)来获取。
噪声和非相关性特征的存在,或特徵尺度与它们的重要性不一致会使K近邻算法的准确性严重降低。对于选取和缩放特征来改善分类已经作了很多研究。一个普遍的做法是利用进化算法优化功能扩展[7],还有一种较普遍的方法是利用训练样本的互信息进行选择特征。
加权最近邻分类器
k- 最近邻分类器可以被视为为 k最近邻居分配权重以及为所有其他邻居分配 0权重。这可以推广到加权最近邻分类器。也就是说,第 i近的邻居被赋予权重,其中。关于加权最近邻分类器的强一致性的类似结果也成立。[9]
设表示权重为的加权最近邻分类器。根据类别分布的规律性条件,超额风险具有以下渐近展开[10]
对常数 and 当 并且 。
最佳加权方案用于平衡上面显示中的两个项,如下所示:令 ,
- 对 并且
- 对 .
利用最优权重,超额风险的渐近展开中的主项是。当使用bagged 最近邻分类器时,类似的结果也是如此。
属性
原始朴素的算法通过计算测试点到存储样本点的距离是比较容易实现的,但它属于计算密集型的,特别是当训练样本集变大时,计算量也会跟着增大。多年来,许多用来减少不必要距离评价的近邻搜索算法已经被提出来。使用一种合适的近邻搜索算法能使K近邻算法的计算变得简单许多。
近邻算法具有较强的一致性结果。随着数据趋于无限,算法保证错误率不会超过贝叶斯算法错误率的两倍[11]。对于一些K值,K近邻保证错误率不会超过贝叶斯的。
连续变量估计
K近邻算法也适用于连续变量估计,比如适用反距离加权平均多个K近邻点确定测试点的值。该算法的功能有:
- 从目标区域抽样计算欧式或马氏距离;
- 在交叉验证后的RMSE基础上选择启发式最优的K邻域;
- 计算多元k-最近邻居的距离倒数加权平均。
發展
然而k最近鄰居法因為計算量相當的大,所以相當的耗時,Ko與Seo提出一演算法TCFP(text categorization using feature projection),嘗試利用特徵投影法來降低與分類無關的特徵對於系統的影響,並藉此提昇系統效能,其實驗結果顯示其分類效果與k最近鄰居法相近,但其運算所需時間僅需k最近鄰居法運算時間的五十分之一。
除了針對文件分類的效率,尚有研究針對如何促進k最近鄰居法在文件分類方面的效果,如Han等人於2002年嘗試利用貪心法,針對文件分類實做可調整權重的k最近鄰居法WAkNN(weighted adjusted k nearest neighbor),以促進分類效果;而Li等人於2004年提出由於不同分類的文件本身有數量上有差異,因此也應該依照訓練集合中各種分類的文件數量,選取不同數目的最近鄰居,來參與分類。
注释
- 这个方案是一个线性插值的推广。
參考文獻
- Altman, N. S. . The American Statistician. 1992, 46 (3): 175–185. doi:10.1080/00031305.1992.10475879.
- Piryonesi S. Madeh; El-Diraby Tamer E. . Journal of Transportation Engineering, Part B: Pavements. 2020-06-01, 146 (2): 04020022. doi:10.1061/JPEODX.0000175.
- Hastie, Trevor. . Tibshirani, Robert., Friedman, J. H. (Jerome H.). New York: Springer. 2001. ISBN 0-387-95284-5. OCLC 46809224.
- Jaskowiak, P. A.; Campello, R. J. G. B. . Brazilian Symposium on Bioinformatics (BSB 2011): 1–8. 已忽略未知参数
|citeseerx=(帮助) - D. Coomans; D.L. Massart. . Analytica Chimica Acta. 1982, 136: 15–27. doi:10.1016/S0003-2670 (01)95359-0 请检查
|doi=值 (帮助). - Everitt, B. S., Landau, S., Leese, M. and Stahl, D.(2011)Miscellaneous Clustering Methods, in Cluster Analysis, 5th Edition, John Wiley & Sons, Ltd, Chichester, UK.
- Nigsch F, Bender A, van Buuren B, Tissen J, Nigsch E, Mitchell JB (2006). "Melting point prediction employing k-nearest neighbor algorithms and genetic parameter optimization". Journal of Chemical Information and Modeling 46 (6): 2412–2422. doi:10.1021/ci060149f. PMID 17125183.
- Hall P, Park BU, Samworth RJ. . Annals of Statistics. 2008, 36 (5): 2135–2152. doi:10.1214/07-AOS537.
- Stone C. J. . Annals of Statistics. 1977, 5 (4): 595–620. doi:10.1214/aos/1176343886.
- Samworth R. J. . Annals of Statistics. 2012, 40 (5): 2733–2763. arXiv:1101.5783. doi:10.1214/12-AOS1049.
- Cover TM, Hart PE (1967). "Nearest neighbor pattern classification". IEEE Transactions on Information Theory 13 (1): 21–27. doi:10.1109/TIT.1967.1053964.
- Bremner D, Demaine E, Erickson J, Iacono J, Langerman S, Morin P, Toussaint G (2005). "Output-sensitive algorithms for computing nearest-neighbor decision boundaries". Discrete and Computational Geometry 33 (4): 593–604. doi:10.1007/s00454-004-1152-0
- E. H. Han, G. Karypis and V. Kumar, Text categorization using weight adjusted k-Nearest Neighbor classification, Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp. 53–65, 2001.
- Y. J. Ko and Y. J. Seo, Text categorization using feature projections, Proceedings of the Nineteenth international conference on Computational linguistics, Volume 1, pp. 1–7, 2002.
- B. L. Li, Q. Lu and S. W. Yu, An adaptive k-nearest neighbor text categorization strategy, ACM Transactions on Asian Language Information Processing, Volume 3 , Issue 4, pp. 215–226, 2004.
拓展阅读
- When Is "Nearest Neighbor" Meaningful?页面存档备份,存于
- Belur V. Dasarathy (编). . 1991. ISBN 0-8186-8930-7.
- Shakhnarovish, Darrell, and Indyk (编). . MIT Press. 2005. ISBN 0-262-19547-X.
- Mäkelä H Pekkarinen A. . Forest Ecology and Management. 2004-07-26, 196 (2–3): 245–255. doi:10.1016/j.foreco.2004.02.049.
- Fast k nearest neighbor search using GPU. In Proceedings of the CVPR Workshop on Computer Vision on GPU, Anchorage, Alaska, USA, June 2008. V. Garcia and E. Debreuve and M. Barlaud.
- Scholarpedia article on k-NN 页面存档备份,存于
- google-all-pairs-similarity-search 页面存档备份,存于
