截角二十面體
在幾何學中,截角二十面體是一種由12個正五邊形和20個正六邊形所組成的凸半正多面體,同時具有每個三面角等角和每條邊等長的性質,因此屬於阿基米德立體[1],但由於其並非所有面全等因此不能算是正多面體。由於其包含了正五邊形和六邊形面,因此也是一種戈德堡多面体[2],其對偶多面體為五角化十二面體。這種結構最早由列奥纳多·达·芬奇給予描述,後來出現於許多藝術創作和學術研究中。自1970年墨西哥足球世界杯之後,這種形狀成為了足球的代表性形狀[3][4],並且會在六邊形塗上白色、五邊形塗上黑色。在科學領域中,這種形狀亦有許多用途,例如建築學家巴克明斯特·富勒提出的網格球頂結構,甚至在核子武器的引爆技術上也有使用這種形狀的設計。巴克明斯特富勒烯分子(C60)也是這種形狀。
| 截角二十面體 | |
|---|---|
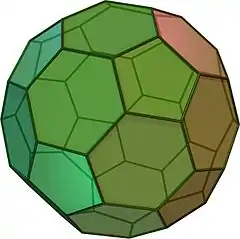 (點選檢視旋轉模型) | |
| 類別 | 阿基米德立體 半正多面體 戈德堡多面體 |
| 面 | 32 |
| 邊 | 90 |
| 頂點 | 60 |
| 歐拉特徵數 | F=32, E=90, V=60 (χ=2) |
| 面的種類 | 正五邊形 正六邊形 |
| 面的佈局 | 12{5}+20{6} |
| 頂點圖 | 5.6.6 |
| 考克斯特符號 | |
| 施萊夫利符號 | t{3,5} t0,1{3,5} |
| 威佐夫符號 | 3 |
| 康威表示法 | tI |
| 對稱群 | Ih, H3, [5,3], (*532), order 120 |
| 參考索引 | U25, C27, W9 |
| 對偶 | 變數 "對偶多面體" 未定義。 |
| 旋轉對稱群 | I, [5,3]+, (532), order 60 |
| 二面角 | 6-6: 138.189685° 6-5: 142.62085° |
| 特性 | 半正、凸 |
 |
 5.6.6 (頂點圖) |
 變數 "對偶多面體" 未定義。 (對偶多面體) |
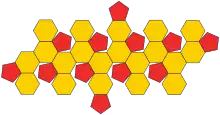
 (展開圖) |
歷史
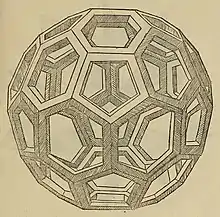 1509年繪製於《De divina proportione》的截角二十面體插圖。 |
這種形狀的骨架結構最早由列奥纳多·达·芬奇給予描述[5],雖然阿基米德被認為是最早想出十三種阿基米德立體的學者,這十三種立體中也包括了截角二十面體[6],但並未留下明確直接提及此形狀的文獻記錄。阿尔布雷希特·丢勒也重現了一個類似截角二十面體的多面體,包含12個五角形和20個六角形面,但是沒有明確的文獻記錄[7][8],不過部分文獻認為這是最早的截角二十面體圖像[9],不過這個時候還沒有「截角」的概念。直到了16、17世紀時,约翰内斯·开普勒才引入了「截角」的概念[9],才得以將這個形狀與正二十面體聯繫起來。自1970年墨西哥世界杯之後,截角二十面體成為足球的代表性形狀。[3][4]
性質
截角二十面體是一種半正多面體,由五邊形和六邊形組成[10],每個頂點都是兩個六邊形和一個五邊形的公共頂點[11],在頂點圖中可計為5.6.6,因此具有點可遞的性質。由於其可以藉由正二十面體透過截角變換,變換而成,因此稱為截角二十面體[12]。由於此原因,截角二十面體在施萊夫利符號中可以用t{3,5}來表示,其中,t表示截角變換,{3,5}表示正二十面體(每個頂點都是五個三角形的公共頂點)。[13]
分類
在幾何學中,截角二十面體是一種半正多面體,由於其具有點可遞的性質,因此屬於阿基米德立體[1]。它由12個正五邊形面、20個正六邊形面、60個頂點和90個邊構成。由於包含了正五邊形和六邊形面因此也是一種戈德堡多面体,在戈德堡符號中可用GPV(1,1) 或 {5+,3}1,1表示[2]。而1983年時,溫尼爾在他的書《多面體模型》中列出許多多面體模型,其中也收錄了此種形狀,並給予編號W9[13]。
組成
截角二十面體共有90條棱和60個頂點[14],正二十面體是由20個正三角形組成。把正二十面體的棱做三等分,則20個正三角形的面就得到了20個正六邊形;同時把正二十面體的所有12個頂點削去[15],則每個頂點由上述三等分點形成的正五邊形代替[12][16]。這就形成了截角二十面體[17]。由於正二十面體有20個正三角形的面,30條棱。每條棱做三等分則有2個分割點,由此削去正二十面體所有12個頂點後得到的截角二十面體有60個頂點。[12]
面的組成
截角二十面體由32個面組成,在這32個面中,共包含了12個正五邊形面和20個正六邊形面,其頂角皆為三面角[18],由2個六邊形和一個五邊形組成,換句話說,即每個頂點都是2個六邊形和一個五邊形的公共頂點,其頂點圖可以計為5.6.6[19]。另外,在這個結構中,五邊形面彼此不相鄰。[20]
 頂點佈局5.6.6 |
尺寸
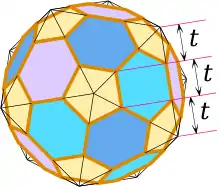
關於截角二十面體的體積,由於截角二十面體已知可以透過切去正二十面體的十二個頂點來構造,並且已知目標立體為等邊多面體,因此可以知道被切下來的12個錐體是等邊正五角錐。所以截角二十面體的體積可以透過正二十面體的體積減去12個錐體是等邊正五角錐來計算[21],其結果為[22]:
- 體積:
而關於截角二十面體的表面積,已知截角二十面體由12個正五邊形和20正六邊形所組成,因此截角二十面體的表面積可以透過12倍正五邊形面積與20倍正六邊形面積的和來計算[21],其結果為[22]:
- 表面積:
正交投影
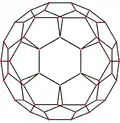
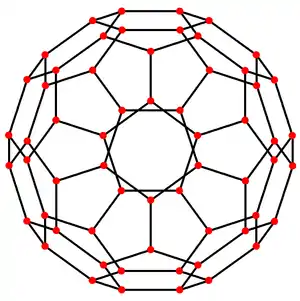
截角二十面體有五種具有特殊對稱性的正交投影,分別是以頂點為中心、以邊為中心(兩種)、以六邊形面為中心以及以五邊形面為中心的正交投影。所述後者兩種正交投影,其對稱性對應於A2 和 H2的考克斯特平面[25][26]。
| 投影位置 | 頂點 | 五邊形-六邊形 稜 |
六邊形-六邊形 稜 |
六邊形面 | 五邊形面 |
|---|---|---|---|---|---|
| 立體 |  |
 |
 | ||
| 圖像 | 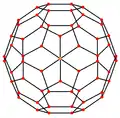 |
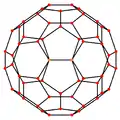 |
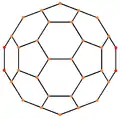 |
 |
 |
| 投影 對稱性 |
[2] | [2] | [2] | [6] | [10] |
| 對偶 |  |
 |
 |
 |
 |
球面鑲嵌
截角二十面體也可以表示為球面鑲嵌,並通過球極投影,投影到平面上。 這個投影是一個等角投影,雖然長度發生改變,但保留了角度資訊。 球面鑲嵌上的直線投影到了平面後成為了弧線。其結果與足球十分相似。[27][16]
 |
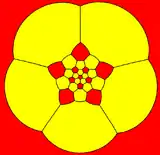 以五邊形為中心 |
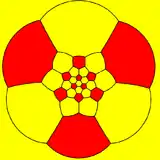 以六邊形為中心 |
| 正交投影 | 球極平面投影 | |
|---|---|---|
應用
截角二十面體在日常生活[3]、藝術、自然科學和技術等領域中皆有用途。
在科學中
在化學中也有一些分子的形狀為截角二十面體,如富勒烯C60[8][28],這種分子於1985年被發現,其直徑約為0.71奈米[29],由60個碳原子組成,且每個碳原子正好位於截角二十面體的頂點上[30]。這種形狀也用於核子武器中,聚焦雷管的爆炸衝擊波用的爆縮透鏡,並配置於小工具和胖子等原子彈中[31][32]。 截角二十面體的一種變體也曾用於由聚合材料製成的窩狀車輪胎框的基礎,其使用了富勒的網格球頂的部分幾何結構(截角二十面體的局部),其被龐蒂克汽車部門在1971年至1976年間用於Trans Am和Grand Prix中[33]。此外,由於這個幾何結構與建築學家巴克明斯特·富勒設計的1967年世界博覽會美國館網格球頂時分相似,為了表達對他的敬意,有時會將其稱為「巴克球」(buckyball)[34]。
相關多面體與鑲嵌
截角二十面體是正二十面體經過截角變換後的結果[24],其他也是由正二十面體透過康威變換得到的多面體有:
| 對稱群: [5,3], (*532) | [5,3]+, (532) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 | |
| {5,3} | t0,1{5,3} | t1{5,3} | t0,1{3,5} | {3,5} | t0,2{5,3} | t0,1,2{5,3} | s{5,3} |
| 半正多面体对偶 | |||||||
 |
 |
 |
 |
 |
 | ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
截角二十面體可視為一種截角的正球面鑲嵌——截角五階三角形鑲嵌,即足球[3]。其他截角正鑲嵌幾何結構包含:
| 截角鑲嵌對稱性 *n32 的變種: n.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n42 [n,3] |
球面鑲嵌 | 歐氏鑲嵌 | 緊湊雙曲 | 仿緊雙曲 | 非緊雙曲 | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | ||
| 截角鑲嵌圖 |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| 頂點 | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| n-kis鑲嵌圖 |  |
 |
 |
 |
 |
 |
 |
|||||
| 頂點 | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
部分均勻星形多面體和一個星形二十面體的凸包為非半正的截角二十面體:[37]
| 凸包為截角二十面體的星形多面體 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
在雙曲空間中,過截角五階十二面體堆砌(Truncated order-5 dodecahedral honeycomb)由截角二十面體獨立堆砌而成,在考克斯特記號中,計為![]()
![]()
![]()
![]()
![]()
![]()
![]() ,其頂點圖為鍥形體。[38][39]
,其頂點圖為鍥形體。[38][39]
在四維空間中,部份多胞體含有截角二十面體形狀的胞,例如大斜方六百胞體(Great rhombated hexacosichoron[40]或稱Cantitruncated 600-cell)和過截角一百二十胞體(Bitruncated 120-cell)。[23]其中大斜方六百胞體共由1440個胞、8640個面、14400條邊和7200個頂點所組成,在其1440個胞中有120個截角二十面體、720個正五角柱和600個截角八面體[41]。而過截角一百二十胞體共由720個胞、4320個面、7200條邊和3600個頂點所組成,在其720個胞中有120個截角二十面體和600個截角四面體[42]。
 大斜方六百胞體 |
 過截角一百二十胞體 |
 (展開圖) |
 (展開圖) |
截角二十面體圖
| 截角二十面體圖 | |
|---|---|
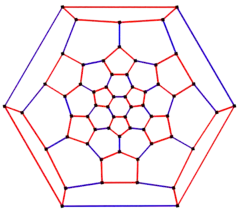 6邊形置中心的施萊格爾圖 | |
| 顶点 | 60 |
| 边 | 90 |
| 自同构群 | 120 |
| 色数 | 3 |
| 属性 | 立方體、哈密顿、正則、零對稱性 |
在圖論的數學領域中,截角二十面體圖是阿基米得立體中截角二十面體之邊與頂點的圖[43],其有時被稱為巴克明斯特富勒圖[44]。共有60個頂點和90條稜,且是立方體的阿基米德圖[45][46][44][43]。
 五摺對稱性 |
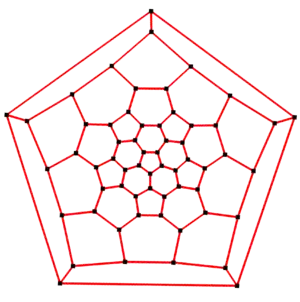 5邊形置中心的施萊格爾圖 |
參見
參考文獻
- Cromwell, P. . United Kingdom: CUP hbk (1997), pbk. (1999), Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2 (英语).
- Magnus Wenninger, , Cambridge University Press, 1979, ISBN 978-0-521-29432-4, MR 552023, (原始内容存档于2008-07-04) (英语) Reprinted by Dover 1999 ISBN 978-0-486-40921-4
- Kotschick, Dieter. . American Scientist. 2006, 94 (4): 350–357. doi:10.1511/2006.60.350 (英语).
- Swart, David; 等, , Proceedings of Bridges 2015: Mathematics, Music, Art, Architecture, Culture (Tessellations Publishing), 2015: 151–158 (英语)
- Saffaro, L. . Taliani, C.; Ruani, G.; Zamboni, R. (编). 2. Singapore: World Scientific. 1992: 55. ISBN 9810210825 (英语).
- Grünbaum, Branko, , Elemente der Mathematik, 2009, 64 (3): 89–101, MR 2520469, doi:10.4171/EM/120 (英语)
- Durer, A. . 1471–1528 (英语).
- Dresselhaus, M. S.; Dresselhaus, G.; Eklund, P. C. . San Diego, CA: Academic Press. 1996. ISBN 012-221820-5 (英语).
- . www2.fkf.mpg.de. [2019-09-10]. (原始内容存档于2017-12-19) (英语).
- Martin Henk. . eg-models.de. 2001-02-01 [2019-09-11] (英语).
- . coolmath.com. [2019-09-10]. (原始内容存档于2019-03-11) (英语).
- Murakami, Hidenori and Nishimura, Yoshitaka. . International Journal of Solids and Structures (Elsevier). 2001, 38 (50-51): 9359––9381 (英语).
- Wenninger, Magnus. . Cambridge University Press. 1974. ISBN 0-521-09859-9 (英语).
- Roman E. Maeder. . MathConsult AG. [2019-09-10]. (原始内容存档于2019-01-16) (英语).
- Kostant, Bertram. . Proceedings of the National Academy of Sciences (National Acad Sciences). 1994, 91 (24): 11714––11717 (英语).
- Paul Bourke, , , Paul Bourke, January 2017 (英语)
- . geom.uiuc.edu. [2019-09-10]. (原始内容存档于2019-03-09) (英语).
- Rene K. Mueller. . simply differently. 2012-10-28 [2019-09-11]. (原始内容存档于2014-10-22) (英语).
- . polyhedra.tessera.li. [2019-09-11] (英语).
- A. Ramachandran, , Azim Premji University At Right Angles, March 2019: 69–71 (英语)
- Harish Chandra Rajpoot Rajpoot, HCR, , Applications of HCR's Theory of Polygon & HCR's formula for platonic solids, 2014 (英语)
- . dmccooey.com. [2018-01-06]. (原始内容存档于2017-12-31) (英语).
- . eusebeia.dyndns.org. [2019-09-10]. (原始内容存档于2019-02-14) (英语).
- {{Cite web |url=http://mathworld.wolfram.com/IcosahedralGroup.html |title=Icosahedral group |website=at MathWorld--A Wolfram Web Resource |publisher=Wolfram Research, Inc. |editor-first=Eric W. |editor-last=Weisstein |editor-link=埃里克·韦斯坦因 |accessdate=2019-09-06 |archive-url=https://web.archive.org/web/20190514160215/{{{mathworlurl}}} |archive-date=2019-05-14 |dead-url=no |quote= |language=en }}
- 約翰·史坦布里奇. . math.lsa.umich.edu. (原始内容存档于2018-02-10) (英语).
- 約翰·史坦布里奇. . math.lsa.umich.edu. (原始内容存档于2017-08-21) (英语).
- Huybers, P, , Int. Conference on Adaptability in Design and Construction, Eindhoven, 2006: 3––5 (英语)
- Kroto, H. W.; Health, J. R.; O'Brien, S. C.; Curl, R. F.; Smalley, R. E. . Nature. 1985, 318 (6042): 162–163. Bibcode:1985Natur.318..162K. doi:10.1038/318162a0 (英语).
- Katz, E. A. . Sōga, Tetsuo (编). . Elsevier. 2006: 364. ISBN 978-0-444-52844-5 (英语).
- Ozaki, Masa-aki and Taahashi, Akira. . Chemical physics letters (Elsevier). 1986, 127 (3): 242––244 (英语).
- Rhodes, Richard. . Touchstone Books. 1996: 195. ISBN 0-684-82414-0 (英语).
- 山田克哉, , ブルーバックス, 講談社, 1996年7月, ISBN 4-06-257128-5, ISBN ISBN 978-4-06-257128-9 (日语)
- Rotella, R. . CarTech. 2018: 64. ISBN 9781613253212. LCCN 2017014572 (英语).
- . Chemical Heritage Foundation. [2016-02-03]. (原始内容存档于2016-01-19) (英语).
- Tarnai, Tibor and Lengyel, András. . Periodica Polytechnica Architecture. 2018, 49 (2): 99––108 (英语).
- Luca Pacioli. . Republic of Venice: Paganini (Venice). 1509 (意大利语).
- Weisstein, Eric W. . MathWorld--A Wolfram Web Resource. [2019-09-06]. (原始内容存档于2018-10-03) (英语).
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294-296) (英文)
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V, p212-213) (英文)
- Richard Klitzing, 4D, uniform polytopes (polychora), (x3x3x5o - grix) (英文)
- . eusebeia.dyndns.org. [2019-09-10]. (原始内容存档于2019-05-03) (英语).
- . eusebeia.dyndns.org. [2019-09-10]. (原始内容存档于2019-02-05) (英语).
- Kostant, Bertram. (PDF). Notices of the AMS. 1995, 42 (9): 959––968 [2018-02-01]. (原始内容存档 (PDF)于2017-01-15) (英语).
- Chris Godsil, Gordon F. Royle. . Graduate Texts in Mathematics. New York: Springer-Verlag. 2001: 211. ISBN 978-0387952208 (英语).
- Read, R. C.; Wilson, R. J., , Oxford University Press: 268, 1998 (英语)
- Weisstein, Eric W. . MathWorld--A Wolfram Web Resource. [2019-09-06]. (原始内容存档于2019-05-18) (英语).
- 參考書目
- Williams, Robert. . Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- Cromwell, P. . United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
外部連結
- 埃里克·韦斯坦因, 截角二十面體 (參閱阿基米德立體) 於MathWorld(英文)
- Richard Klitzing, 3D convex uniform polyhedra, x3x5o - ti
- Editable printable net of a truncated icosahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- 3D paper data visualization World Cup ball