代數整數
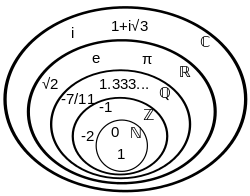
在數學裡,代數整數(algebraic integer)是複數中的一类。一个複数α是代数整数当且仅当它是某个個整系數的首一多項式的根。其中首一(英文:monic)意謂最高冪次項的系數是1。
| 的数 | ||
| 基本 | ||
|
| ||
| 延伸 | ||
|
| ||
| 其他 | ||
|
|
因此,所有代數整數都是代數數,但並非所有代數數都是代數整數。所有代数整数构成一个环,通常记作。
如果是整係數本原多項式(即系數的最大公因数是1的多项式),但非首一多項式,則的根都不是代數整數。
定义
以下是代数整数四种相互等价的定义。设K为代数数域(有理数域的有限扩张)。根据本原元定理,K可以写成的形式。其中是某个代数数。设有,则α是代数整数当且仅当以下命题之一成立:
- 存在整系数多项式:,使得。
- α在上的极小首一多项式是整系数多项式。
- 是有限生成的-模。
- 存在有限生成的-子模:,使得。
例子
- 有理数域中的代数整数就是整数。换句话说,和交集是整数环。这可以用整系数多项式的一个简单性质证明。如果一个整系数多项式
- 有一个根是有理数:,其中p、q是互素的整数,那么必然有:分母q 整除,以及分子p 整除。因此,由于代数整数是某个首一多项式的根,如果它是有理数,那么它的分母整除多项式的最高冪次項,也就是说整除1。所以这个有理数的分母是1,即是说它是整数。反过来,所有的整数n都是整系数首一多项式的根,所以是代数整数。
- 一个给定的代数数域与的交集称为这个数域的(代数)整数环,记作。这个整数环中的代数整数不再只是整数。比如说,给定一个数域:,那么对应的整数环中不仅有整数,还有,因为是首一多项式的根。
- 不是代数整数。这是因为在有理数域上的最小多项式是,不是一个首一多项式。
- 是一个代数整数。它是多项式的根。一般来说,如果整数除以4余1,那么也是代数整数,因为它是多项式的根。
性质
参考来源
- Daniel A. Marcus, Number Fields(数域), third edition, Springer-Verlag, 1977
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.