微积分基本定理
定理的第一部分,称为微积分第一基本定理,此定理表明:給定任一連續函數,可以(利用積分)構造出了該函數的反導函數。這一部分定理的重要之處在於它保證了連續函數的反導函數的存在性。
| 系列條目 | |||||
| 微积分学 | |||||
|---|---|---|---|---|---|
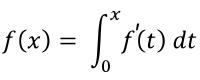 | |||||
| |||||
|
基础概念(含极限论和级数论)
|
|||||
|
一元微分
|
|||||
|
多元微积分
|
|||||
微积分基本定理描述了微积分的两个主要运算──微分和积分之间的关系。
定理的第二部分,称为微积分第二基本定理或牛顿-莱布尼茨公式,表明某函數的定积分可以用該函數的任意一個反導函數来计算。这一部分是微積分或數學分析中相當關鍵且應用很廣的一個定理,因为它大大简化了定积分的计算。[1]
该定理的一个特殊形式,首先由詹姆斯·格里高利(1638-1675)证明和出版。[2]定理的一般形式,则由艾萨克·巴罗完成证明。
對微积分基本定理比較直觀的理解是:把函數在一段區間的「无穷小变化」全部「加起來」,會等于该函數的净变化,這裡「無窮小變化」就是微分,「加起來」就是積分,淨變化就是該函數在區間兩端點的差。
我们从一个例子开始。假设有一个物体在直线上运动,其位置为x(t),其中t为时间,x(t)意味着x是t的函数。这个函数的导数等于位置的无穷小变化dx除以时间的无穷小变化dt(当然,该导数本身也与时间有关)。我们把速度定义为位置的变化除以时间的变化。用莱布尼兹记法:
整理,得
根据以上的推理,的变化──,是的无穷小变化之和。它也等于导数和时间的无穷小乘积之和。这个无穷的和,就是积分;所以,一个函数求导之后再积分,得到的就是原来的函数。我们可以合理地推断,这个运算反过来也成立,积分之后再求导,得到的也是原来的函数。
历史
詹姆斯·格里高利首先发表了该定理基本形式的几何证明[3][4][5],艾萨克·巴罗证明了该定理的一般形式[6] 。巴罗的学生艾萨克·牛顿使微积分的相关理论得以完善。莱布尼茨使得相关理论实现体系化并引入了沿用至今微积分符号,
正式表述
證明
第一部分
假设有
设x1和x1 + Δx为区间[a, b]中的两个数。我们有
和
两式相减,得
可以证明
- (两个相邻区域的面积之和,等于两个区域合并起来的面积。)
整理,得
把上式代入(1),得
根据积分第一中值定理,在区间(x1, x1 + Δx)存在一个c,使得
把上式代入(2),得
两边除以Δx,得
- 注意左边的表达式是F在x1处的牛顿差商。
两边取Δx → 0的极限,
左边的表达式是F在x1处的导数的定义。
我们用夹挤定理来求另一个极限。c在区间[x1, x1 + Δx]内,因此x1 ≤ c ≤ x1 + Δx。
另外 and
所以,根据夹挤定理,
代入(3),可得
函数f在c处连续,所以极限可以在函数里面进行。因此,我们有
证明完毕。
第二部分
设f在区间[a, b]上连续,并设F为f的原函数。我们从以下表达式开始
设有数
- x0, ..., xn
使得
可得
我们加上F(xi)及其相反数,这样等式仍成立:
以上表达式可用以下的和表示:
我们将使用均值定理。就是:
设F在闭区间[a, b]连续,在开区间(a, b)可导,则开区间(a, b)内一定存在c使得
可得
函数F在区间[a, b]可导,所以在每一个区间xi-1也是可导和连续的。因此,根据均值定理,
把上式代入(1),得
根据第一部分的结论,我们有。另外,可表示为第个小区间的。

注意到我们正在描述矩形的面积(长度乘以宽度),并把这些面积相加起来。每一个矩形都描述了一部分曲线的估计。同时也注意到,并不需要对于任何都是相同的,换句话说,矩形的长度可以变化。我们要做的,是要用个矩形来近似代替曲线。现在,当n增加而每一个矩形越来越小时,它的面积就越来越接近曲线的真实面积。
当矩形的宽度趋近于零时取极限,便得出黎曼积分。也就是说,我们取最宽的矩形趋于零,而矩形的数目趋于无穷大时的极限。
所以,我们把(2)式的两边取极限,得
F(b)和F(a)都不依赖于||Δ||,所以左面的极限仍然是F(b) - F(a)。
右边的表达式定义了f从a到b的积分。这样,我们有
证明完毕。
例子
计算以下积分:
在这里,,是一个原函数。因此:
推广
我们不需要假设 f 在整个区间是连续的。这样定理的第一部分便说明:如果 f 是区间[a, b]内的任何一个勒贝格可积的函数,x0是[a, b]内的一个数,使得 f 在 x0连续,则
在x = x0是可导的,且F'(x0) = f(x0)。我们可以把f的条件进一步降低,假设它仅仅是可积的。这种情况下,我们便得出结论:F几乎处处可导,且F'(x)几乎处处等于f(x)。这有时称为勒贝格微分定理。
定理的第一部分对于任何具有原函数F的勒贝格可积函数f都是正确的(不是所有可积的函数都有原函数)。
泰勒定理中把误差项表示成一个积分的形式,可以视为微积分基本定理的一个推广。
对于复数函数,也有一个类似的形式:假设U是C的一个开集,f: U → C是一个在U处具有全纯原函数F的函数。那么对于所有曲线γ: [a, b] → U,曲线积分可以用下式来计算:
微积分基本定理可以推广到多维空间的曲线和曲面积分,也可以推广到流形。
这个方向上的一个有力的表述是斯托克斯定理:设 M 为一个可定向分段光滑n维流形,并设为n−1阶M上的C1类紧支撑微分形式。如果∂M表示M的边界,并以M的方向诱导的方向为边界的方向,则
注解
- 更加确切地,该定理涉及了可变上限和任意选择的下限的定积分。这类特殊的定积分允许我们计算函数的无穷多个原函数之一(除了那些没有零点的原函数)因此,它几乎跟不定积分是等价的,大部分作者把它定义为产生任何一个可能的原函数的运算,包括没有零点的原函数。
- See, e.g., Marlow Anderson, Victor J. Katz, Robin J. Wilson, Sherlock Holmes in Babylon and Other Tales of Mathematical History, Mathematical Association of America, 2004, p. 114.
- Malet, Antoni. . Archive for History of Exact Sciences (Springer-Verlag). 1993. doi:10.1007/BF00375656.
Gregorie's thought, on the other hand, belongs to a conceptual framework strongly geometrical in character. (page 137)
- See, e.g., Marlow Anderson, Victor J. Katz, Robin J. Wilson, Sherlock Holmes in Babylon and Other Tales of Mathematical History, Mathematical Association of America, 2004, p. 114.
- Gregory, James. . Museo Galileo: Patavii: typis heredum Pauli Frambotti. 1668.
- Child, James Mark; Barrow, Isaac. . Chicago: Open Court Publishing Company. 1916.
参考文献
- Larson, Ron, Bruce H. Edwards, David E. Heyd. Calculus of a single variable. 7th ed. Boston: Houghton Mifflin Company, 2002.
- Leithold, L. (1996). The calculus 7 of a single variable. 6th ed. New York: HarperCollins College Publishers.
- Malet, A, Studies on James Gregorie (1638-1675) (PhD Thesis, Princeton, 1989).
- Stewart, J. (2003). Fundamental Theorem of Calculus. In Integrals. In Calculus: early transcendentals. Belmont, California: Thomson/Brooks/Cole.
- Turnbull, H W (ed.), The James Gregory Tercentenary Memorial Volume (London, 1939)
.gif)